练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在棋盘中建立如图的直角坐标系，三颗棋子A，O，B的位置如图，它们分别是(－1，1)，(0，0)和(1，0)．

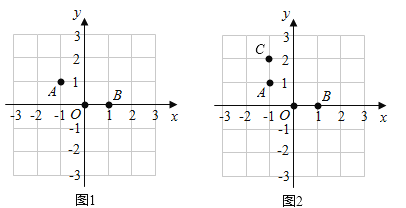
    (1)如图2，添加棋子C，使A，O，B，C四颗棋子成为一个轴对称图形，请在图中画出该图形的对称轴；

    (2)在其他格点位置添加一颗棋子P，使A，O，B，P四颗棋子成为一个轴对称图形，请直接写出棋子P的位置的坐标．(写出2个即可)

    【答案】(1)见解析 (2) P(0，－1)，P′(－1，－1)

    【解析】（1）根据A，B，O，C的位置，结合轴对称图形的性质进而画出对称轴即可；

    （2）利用轴对称图形的性质得出P点位置．

    （1）如图2所示，C点的位置为（-1，2），A，O，B，C四颗棋子组成等腰梯形，直线l为该图形的对称轴；

    （2）如图1所示：P（0，-1），P′（-1，-1）都符合题意．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，已知A，B分别为数轴上的两点，点A表示的数是﹣30，点B表示的数是50．

    （1）请写出线段AB中点M表示的数是　 　．

    （2）现有一只蚂蚁P从点B出发，以每秒3个单位长度的速度沿数轴向左移动，同时另一只蚂蚁Q恰好从点A出发，以每秒2个单位长度的速度沿数轴向右移动，设两只蚂蚁在数轴上的点C相遇．

    ①求A、B两点间的距离；

    ②求两只蚂蚁在数轴上的点C相遇时所用的时间；

    ③求点C对应的数是多少？

    （3）若蚂蚁P从点B出发，以每秒3个单位长度的速度沿数轴向左运动，同时另一只蚂蚁恰好从A点出发，以每秒2个单位长度的速度沿数轴也向左运动，设两只蚂蚁在数轴上的D点相遇，求D点表示的数是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（原题）已知直线AB∥CD，点P为平行线AB，CD之间的一点．如图1，若∠ABP=50°，∠CDP=60°，BE平分∠ABP，DE平分∠CDP，求∠BED的度数．

    （探究）如图2，当点P在直线AB的上方时，若∠ABP=α，∠CDP=β，∠ABP和∠CDP的平分线交于点E1，∠ABE1与∠CDE1的角平分线交于点E2，∠ABE2与∠CDE2的角平分线交于点E3，…以此类推，求∠En的度数．

    （变式）如图3，∠ABP的角平分线的反向延长线和∠CDP的补角的角平分线交于点E，试猜想∠P与∠E的数量关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在梯形,,过点，垂足为，并延长，使，联结.

    （1）求证：四边形是平行四边形。

    （2）联结，如果

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】现有一根长为1米的木杆，第1次截取其长度的一半，第2次截取其第1次剩下长度的一半，第3次截取其第2次剩下长度的一半，如此反复截取，则第n（n为正整数）次截取后，此木杆剩下的长度为米．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】6月5日是“世界环境日”，南宁市某校举行了“绿色家园”演讲比赛，赛后整理参赛同学的成绩，制作成直方图(如图)．

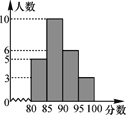
    (1)全校共有多少人参加比赛？

    (2)组距是多少？组数是多少？

    (3)分数段在哪个范围内的人数最多？并求出该小组的频数、频率；

    (4)如果比赛成绩90分以上(含90分)可以获得奖励，那么获奖率是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了考查一种零件的加工精度，从中抽出40只进行检测，其尺寸数据如下(单位：微米)：

    161，165，164，166，160，158，163，162，168，159，

    147，165，167，151，164，159，152，159，149，172，

    162，157，162，169，156，164，163，157，163，165，

    173，159，157，169，165，154，153，163，168，169.

    试列出样本频数及频率分布表，绘制频数分布直方图．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，平行四边形ABCD的对角线AC，BD交于点O，过点B作BP∥AC，过点C作CP∥BD，BP与CP相交于点P．

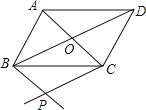
    （1）判断四边形BPCO的形状，并说明理由；

    （2）若将平行四边形ABCD改为菱形ABCD，其他条件不变，得到的四边形BPCO是什么四边形，并说明理由；

    （3）若得到的是正方形BPCO，则四边形ABCD是 ．（选填平行四边形、矩形、菱形、正方形中你认为正确的一个）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在四边形ABCD中，∠B=∠D=90°，∠BAD=105°，在BC，CD上分别找一点M、N，使得△AMN周长最小，则∠AMN+∠ANM的度数为 （ ）

    A. 100° B. 105° C. 120° D. 150°

    查看答案和解析>>

    同步练习册答案