练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
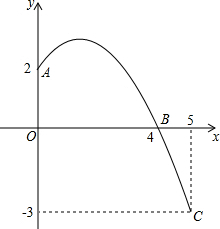
    18．已知：如图是抛物线y=ax2+bx+c（a≠0）的一部分，且图象经过A，B，C三点，求抛物线的解析式．

    分析 将A、B、C三点分别代入一般式y=ax2+bx+c，然后解方程组即可求得解析式．

    解答 解：因为y=ax2+bx+c的图象经过A（0，2），C（4，0），B（5，-3）三点，
    ∴$\left\{\begin{array}{l}{c=2}\\{16a+4b+c=0}\\{25a+5b+c=-3}\end{array}\right.$，
    解得：a=-$\frac{1}{2}$，b=$\frac{3}{2}$，c=2．
    因此这个二次函数的解析式是 y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2．

    点评 此题主要考查了待定系数法求二次函数解析式和二次函数图象的知识点，熟练掌握待定系数法是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    8．已知三个有理数a，b，c的积是正数，它们的和是负数，当x=$\frac{|a|}{a}+\frac{|b|}{b}+\frac{|c|}{c}$时，求代数式：-3x19-2008x-2013的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．用计算器计算并填空．
    ①11-2=9=（　　）2
    ②1111-22=1089=（　　）2
    ③111111一222=110889=（　　）2 
    ④11111111-2222=11108889=（　　）2
    （1）你发现了什么规律？
    （2）不用计算器，$\underset{\underbrace{111…111}}{2006个}-\underset{\underbrace{222…222}}{1003个}$=（　　）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．如图，抛物线顶点坐标是P（1，2），函数y随自变量x的增大而减小的x的取值范围是（　　）
    A．x＞2B．x＜2C．x＞1D．x＜1

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．在式子$\frac{ab}{3}$，4t2，0，$\frac{1}{x}$，3.5x，m+1，2（a+1），$\frac{3xy}{π}$中，单项式有（　　）
    A．3个B．4个C．5个D．6个

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．计算下列各式的结果，填在横线上．
    （1）（-2）+（+2）=0；
    （2）（-19）+（+19）=0；
    （3）（+70）+（-70）=0；
    （4）100+（-100）=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．下列各组条件中，能判定△ABC≌△DEF的是（　　）
    A．AB=DE，BC=EF，∠A=∠DB．∠A=∠D，∠C=∠F，AC=EF
    C．AB=DE，BC=EF，AC=DFD．∠B=∠E

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．定义a※b=a2-b，则1※2=-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．如图，在△ABC中，AB=3cm，AC=4cm，AD是BC的中线，DE，DF分别是△ABD和△ACD的高，求DE：DF的值．

    查看答案和解析>>

    同步练习册答案