
【题目】小明和小刚进行赛跑训练,他们选择了一个土坡,按同一路线同时出发,从坡脚跑到坡顶再原路返回坡脚.他们俩上坡的平均速度不同,下坡的平均速度则是各自上坡平均速度的1. 5倍.设两人出发x min后距出发点的距离为y m.图中折线段OBA表示小明在整个训练中y与x的函数关系,其中点A在x轴上,点B坐标为(2,480).
(1)点B所表示的实际意义是 ;
(2)求出AB所在直线的函数关系式;
(3)如果小刚上坡平均速度是小明上坡平均速度的一半,那么两人出发后多长时间第一次相遇?

【答案】(1)、小明出发2分钟跑到坡顶,此时离坡脚480米;(2)、y=-360x+1200;(3)、2.5min.
【解析】
试题分析:(1)、根据函数图象得出点B的实际意义;(2)、首先求出上坡的速度,然后得出下坡的速度已经点A的坐标;利用待定系数法求出函数解析式;(3)、首先求出小刚上坡的速度,然后进行计算.
试题解析:(1)、小明出发2分钟跑到坡顶,此时离坡脚480米;
(2)、小明上坡的平均速度为480÷2=240(m/min) 则其下坡的平均速度为:240×1.5=360(m/min),
故回到出发点时间为2+480÷360=(min), ∴A点坐标为(![]() ,0),
,0),
设y=kx+b,将B(2,480)与A(![]() ,0)代入得:
,0)代入得: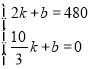 解得:
解得:![]()
∴y=-360x+1200.
(3)、小刚上坡的平均速度为240×0.5=120(m/min),小明的下坡平均速度为240×1.5=360(m/min),由图像得小明到坡顶时间为2分钟,
此时小刚还有480-2×120=240m没有跑完, 两人第一次相遇时间为2+240÷(120+360)=2.5(min).


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:
【题目】已知a+b=5,ab=3,则a2+b2=______.
【答案】19
【解析】试题分析:a2+b2=(a+b)2-2ab=25-6=19.
考点:完全平方公式的应用.
【题型】填空题
【结束】
16
【题目】分解因式2a(b+c)-3(b+c)的结果是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年舌尖上的浪费让人触目惊心,据统计中国每年浪费的食物总量折合粮食约499.5亿千克,这个数用科学记数法应表示为( )
A. 4.995×1010B. 49.95×1010
C. 0.4995×1011D. 4.995×1011
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知E,F分别为正方形ABCD的边BC,CD上的点,AF,DE相交于点G,当E,F分别为边BC,CD的中点时,有:①AF=DE;②AF⊥DE成立.
试探究下列问题:
(1)如图1,若点E不是边BC的中点,F不是边CD的中点,且CE=DF,上述结论①,②是否仍然成立?(请直接回答“成立”或“不成立”),不需要证明)
(2)如图2,若点E,F分别在CB的延长线和DC的延长线上,且CE=DF,此时,上述结论①,②是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由;
(3)如图3,在(2)的基础上,连接AE和EF,若点M,N,P,Q分别为AE,EF,FD,AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车制造厂开发一款新式电动汽车,计划一年生产安装240辆.由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人.他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门发现:1名熟练工和2名新工人每月可安装8辆电动汽车;2名熟练工和3名新工人每月可安装14辆电动汽车.
(1)每名熟练工和新工人每月分别可以安装多少辆电动汽车?
(2)如果工厂招聘n(0<n<10)名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,那么工厂有哪几种新工人的招聘方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=﹣x2+bx+c与x轴交于A(2,0),B(﹣4,0)两点.
(1)求该抛物线的解析式;
(2)若抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
(3)在抛物线的第二象限图象上是否存在一点P,使得△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若不存,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com