
【题目】如图,某住宅小区在施工过程中留下了一块空地(图中的四边形ABCD),经测量,在四边形ABCD中,AB=3 m,BC=4 m,CD=12 m,DA=13 m,∠B=90°.小区为美化环境,欲在空地上铺草坪,已知草坪每平方米30元,试问铺满这块空地共需花费多少元?

科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想
图1中,线段PM与PN的数量关系是 ,位置关系是 ;
(2)探究证明
把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
(3)拓展延伸
把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着科技进步,无人机的应用越来越广,如图1,在某一时刻,无人机上的探测器显示,从无人机A处看一栋楼顶部B点的仰角和看与顶部B在同一铅垂线上高楼的底部C的俯角.

(1)如果上述仰角与俯角分别为30°与60°,且该楼的高度为30米,求该时刻无人机的竖直高度CD;
(2)如图2,如果上述仰角与俯角分别为α与β,且该楼的高度为m米.求用α、β、m表示该时刻无人机的竖直高度CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新知学习,若一条线段把一个平面图形分成面积相等的两部分,我们把这条段线做该平面图形的二分线解决问题:
(1)①三角形的中线、高线、角平分线中,一定是三角形的二分线的是_______
②如图1,已知△ABC中,AD是BC边上的中线,点E,F分别在AB,DC上,连接EF,与AD交于点G,若![]() 则EF_____(填“是”或“不是”)△ABC的一条二分线.并说明理由.
则EF_____(填“是”或“不是”)△ABC的一条二分线.并说明理由.

(2)如图2,四边形ABCD中,CD平行于AB,点G是AD的中点,射线CG交射线BA于点E,取EB的中点F,连接CF.求证:CF是四边形ABCD的二分线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,甲车到达C地后因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图2,结合图象信息解答下列问题:
(1)乙车的速度是 千米/时,乙车行驶的时间t= 小时;
(2)求甲车从C地按原路原速返回A地的过程中,甲车距它出发地的路程y与它出发的时间x的函数关系式;
(3)直接写出甲车出发多长时间两车相距80千米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,AB=6,AC=8,BC=11,任作一条直线将△ABC分成两个三角形,若其中有一个三角形是等腰三角形,则这样的直线最多有( )
A.5条B.6条C.7条D.8条
查看答案和解析>>
科目:初中数学 来源: 题型:
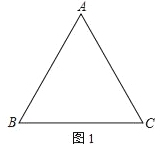
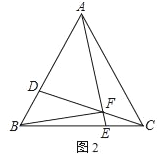
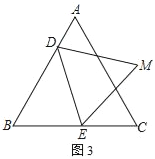
【题目】如图,△ABC是边长为6cm的等边三角形,点D从B点出发沿B→A方向在线段BA上以a cm/s速度运动,与此同时,点E从线段BC的某个端点出发,以b cm/s速度在线段BC上运动,当D到达A点后,D、E运动停止,运动时间为t(秒).
(1)如图1,若a=b=1,点E从C出发沿C→B方向运动,连AE、CD,AE、CD交于F,连BF.当0<t<6时:
①求∠AFC的度数;
②求![]() 的值;
的值;
(2)如图2,若a=1,b=2,点E从B点出发沿B→C方向运动,E点到达C点后再沿C→B方向运动.当t≥3时,连DE,以DE为边作等边△DEM,使M、B在DE两侧,求M点所经历的路径长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com