
 已知,如图抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=4OB.
已知,如图抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=4OB.分析 (1)根据点B的坐标为(1,0),OC=4OB可得出C点坐标,再把BC两点的坐标代入抛物线y=ax2+3ax+c(a>0)求出a,c的值即可;
(2)过点D作DM∥y轴分别交线段AC和x轴于点M,N,利用待定系数法求出直线AC的解析式,故可得出DM=-(x+2)2+4,再由S四边形ABCD=S△ABC+S△ACD即可得出结论;
(3)①过点C作CP1∥x轴交抛物线于点P1,过点P1作P1E1∥AC交x轴于点E1,此时四边形ACP1E1为平行四边形,根据PC两点的纵坐标相等可得出P点坐标;②平移直线AC交x轴于点E,交x轴上方的抛物线于点P,当AC=PE时,四边形ACEP为平行四边形,令P(x,4),由x2+3x-4=4得出x的值即可得出P点坐标.
解答  解:(1)∵OC=4OB,B(1,0),
解:(1)∵OC=4OB,B(1,0),
∴C(0,-4).
把点B,C的坐标代入y=ax2+3ax+c,得a+3a+c=0,c=-4,
解得a=1,c=-4,
∴抛物线线的解析式为:y=x2+3x-4;
(2)如图1,过点D作DM∥y轴分别交线段AC和x轴于点M,N.
∵抛物线线的解析式为y=x2+3x-4,
∴A(-4,0),
∴AB=5,
∴S四边形ABCD=S△ABC+S△ACD=$\frac{1}{2}$AB×OC++$\frac{1}{2}$×DM×(AN+ON)=10+$\frac{1}{2}$×DM×(AN+ON)=10+2DM,
设直线AC的解析式为y=kx+b(k≠0),
∵A(-4,0),C(0,-4),
∴$\left\{\begin{array}{l}-4k+b=0\\ b=-4\end{array}\right.$,解得$\left\{\begin{array}{l}k=-1\\ b=-4\end{array}\right.$,
故直线AC的解析式为:y=-x-4.
令D(x,x2+3x-4),M(x,-x-4),则DM=-x-4-(x2+3x-4)=-(x+2)2+4,
当x=-2时,DM有最大值4,此时四边形ABCD面积有最大值为18;
另解:连接OD令D(x,x2+3x-4),
∵A(-4,0),B(1,0),C(0,-4),
∴S四边形ABCD=S△OBC+S△AOD+S△OCD
=$\frac{1}{2}$OB•OC+$\frac{1}{2}$OA•|x2+3x-4|+$\frac{1}{2}$OC|x|
=$\frac{1}{2}$×1×4-$\frac{1}{2}$×4×(x2+3x-4)-$\frac{1}{2}$×4x
=-(x+2)2+18,
∴当x=-2时,此时四边形ABCD面积有最大值为18;
(3)①如图2,过点C作CP1∥x轴交抛物线于点P1,过点P1作P1E1∥AC交x轴于点E1,此时四边形ACP1E1为平行四边形.
∵C(0,-4),令x2+3x-4=-4,
∴x=0或x=-3.
∴P1(-3,-4).
②如图3,平移直线AC交x轴于点E,交x轴上方的抛物线于点P,当AC=PE时,四边形ACEP为平行四边形,
∵C(0,-4),
∴可令P(x,4),由x2+3x-4=4,得x2+3x-8=0.
解得x=-3+$\sqrt{41}$或x=-3-$\sqrt{41}$.
此时存在点P2(-3+$\sqrt{41}$,4)和P3(-3-$\sqrt{41}$,4)
综上所述,存在3个点符合题意,坐标分别是P1(-3,-4),P2(-3+$\sqrt{41}$,4),P3(-3-$\sqrt{41}$,4).
点评 本题考查的是二次函数综合题,涉及到用待定系数法求一次函数及二次函数的解析式、平行四边形的判定与性质等知识,在解答(3)时要注意进行分类讨论.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
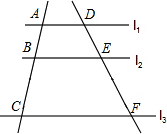 如图,l1∥l2∥l3,如果AB=2,BC=3,DF=4,那么DE=( )
如图,l1∥l2∥l3,如果AB=2,BC=3,DF=4,那么DE=( )| A. | $\frac{4}{3}$ | B. | $\frac{5}{4}$ | C. | $\frac{8}{5}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年四川省长宁县双河学区八年级下学期第一次联考数学试卷(解析版) 题型:解答题
已知一次函数y=ax-3a2+12,请按要求解答问题:
(1)a为何值时,函数图象过原点,且y随x的增大而减小?
(2)若函数图象平行于直线y=-x,求一次函数的表达式;
(3)若点(0,-15)在函数图象上,求a的值
查看答案和解析>>
科目:初中数学 来源:2017届四川省遂宁市九年级上学期期末考试数学试卷(解析版) 题型:单选题
如图,在△ABC中,∠ABC=90°,DE垂直平分AC,垂足为O,AD∥BC,且AB=3,BC=4,则AD的长为( )

A. 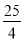 B.
B.  C.
C. 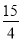 D.
D. 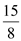
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com