
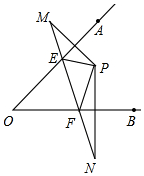
 如图,点P在∠AOB内,点M、N分别是P点关于OA、OB的对称点,且MN交OA、OB相交于点E,若△PEF的周长为20,求MN的长.
如图,点P在∠AOB内,点M、N分别是P点关于OA、OB的对称点,且MN交OA、OB相交于点E,若△PEF的周长为20,求MN的长. 科目:初中数学 来源: 题型:解答题
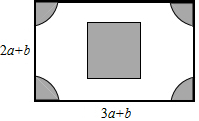 如图,有一块长(3a+b)米,宽(2a+b)米的长方形广场,园林部门要对阴影区域进行绿化,空白区域进行广场硬化,其中,四个角部分是半径为(a-b)米的四个大小相同的扇形,中间部分是边长为(a+b)米的正方形.
如图,有一块长(3a+b)米,宽(2a+b)米的长方形广场,园林部门要对阴影区域进行绿化,空白区域进行广场硬化,其中,四个角部分是半径为(a-b)米的四个大小相同的扇形,中间部分是边长为(a+b)米的正方形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
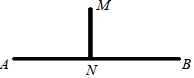 如图所示,把河水引向水池M,要向水池M点向河岸AB画垂线,垂足为N,再沿垂线MN开一条渠道才能使渠道最短.其依据是( )
如图所示,把河水引向水池M,要向水池M点向河岸AB画垂线,垂足为N,再沿垂线MN开一条渠道才能使渠道最短.其依据是( )| A. | 垂线段最短 | |
| B. | 过一点确定一条直线与已知直线垂直 | |
| C. | 两点之间线段最短 | |
| D. | 以上说法都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示是某台阶的一部分,如果点A的坐标为(0,0),B点的坐标为(1,1).
如图所示是某台阶的一部分,如果点A的坐标为(0,0),B点的坐标为(1,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com