练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
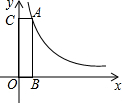
    6．如图，过反比例函数y=$\frac{4}{x}$（x＞0）上一点A作AB⊥x轴于点B，AC⊥y轴于点C，则四边形OBAC的面积是（　　）
    A．2B．4C．6D．8

    分析 根据题意可以先设出点A的坐标，然后根据矩形的面积公式即可解答本题．

    解答 解：设点A的坐标为（a，$\frac{4}{a}$），
    ∵AB⊥x轴于点B，AC⊥y轴于点C，
    ∴四边形OBAC是矩形，
    ∴四边形OBAC的面积是：a$•\frac{4}{a}$=4，
    故选B．

    点评 本题考查反比例函数系数k的几何意义，解答本题的关键是明确题意，找出所求问题需要的条件，利用反比例函数的性质和数形结合的思想解答．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    13．点A的坐标是（-1，-3），则点A在（　　）
    A．第一象限B．第二象限C．第三象限D．第四象限

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

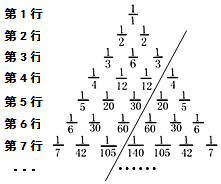    17．如图是“分数三角形”数表，记第i行从左往右数第j个数为ai，j（其中i、j均为正整数且j≤i），如a5，2=$\frac{1}{20}$，a7，6=$\frac{1}{42}$；请认真观察此数表的规律并完成下列作答．
    （1）第10行的第一个数为$\frac{1}{10}$，第10行的第二个数为$\frac{1}{90}$；
    （2）我发现了此数表有以下规律：
    ①第i行的第一个数与最后一个数均为$\frac{1}{i}$（用字母i来表示）；
    ②请仔细观察每行相邻两个数与它们头顶上的那个数的关系，并完成下面填空：ai，2+ai，3=a（i-1），2（其中i为正整数且i≥3）；
    （3）请利用第（2）问②的规律计算：$\frac{1}{3}+\frac{1}{12}+\frac{1}{30}+\frac{1}{60}+\frac{1}{105}$．（请给出运算过程）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

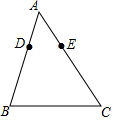    14．如图，在△ABC中，已知D、E分别是AB、AC边上的点，且AD=3，AB=8，AC=10，若△ADE与△ABC相似，则AE的长为（　　）
    A．$\frac{15}{4}$B．$\frac{4}{15}$或$\frac{12}{5}$C．$\frac{15}{4}$或$\frac{12}{5}$D．$\frac{5}{12}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

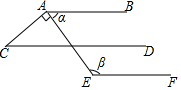    1．如图，∠α和∠β的度数满足方程组$\left\{\begin{array}{l}{2α+β=230}\\{3α-β=20}\end{array}\right.$．
    （1）求∠α和∠β的度数，并判断AB与EF的位置关系；
    （2）若CD∥EF，AC⊥AE，求∠C的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．不透明的袋子中装有10个黑球、1个白球，它们除颜色外无其它差别，随机从袋子中摸出一个球，则（　　）
    A．这个球一定是黑球B．事先能确定摸到什么颜色的球
    C．这个球可能是白球D．摸到黑球、白球的可能性大小一样

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．下列各式运算正确的是（　　）
    A．a2+a3=a5B．a10÷a2=a5C．（ab2）3=ab6D．a2•a3=a5

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．下列图形中，不是轴对称图形的是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．如果直线y=kx+b经过一、二、四象限，则k，b的取值分别是（　　）
    A．k＞0，b＞0B．k＞0，b＜0C．k＜0，b＞0D．k＜0，b＜0

    查看答案和解析>>

    同步练习册答案