
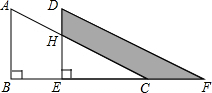
 如图,将Rt△ABC沿射线BC方向平移得到△DEF,已知AB=16cm,BE=10cm,DH=6cm,则图中阴影部分的面积为130cm2.
如图,将Rt△ABC沿射线BC方向平移得到△DEF,已知AB=16cm,BE=10cm,DH=6cm,则图中阴影部分的面积为130cm2. 分析 根据平移的性质可得DE=AB,然后求出HE,再判断出阴影部分的面积等于四边形ABEH的面积,最后利用梯形的面积公式列式计算即可得解.
解答 解:∵将Rt△ABC沿射线BC方向平移得到△DEF,
∴DE=AB=16cm,
∵DH=6cm,
∴HE=DE-DH=10cm,
∵∠B=90°,
∴四边形ABEH是梯形,
S阴影=S△DEF-S△CEH=S△ABC-S△CEH=S梯形ABEH
=$\frac{1}{2}$(AB+HE)•BE
=$\frac{1}{2}$×(16+10)×10
=130(cm2).
故答案为:130cm2.
点评 本题考查平移的基本性质:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等;本题判断出阴影部分的面积与四边形的面积相等是解题的关键.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,一段抛物线:y=x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A,将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…,如此进行下去,直至得C673.若P(2017,a)在第673段抛物线C673上,则a=-2.
如图,一段抛物线:y=x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A,将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…,如此进行下去,直至得C673.若P(2017,a)在第673段抛物线C673上,则a=-2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com