

分析 (1)根据旋转得出△QAQ'是等边三角形,解答即可;
(2)根据旋转的性质得出构成的四边形是平行四边形,证明即可;
应用:(1)根据旋转得出构成的四边形是矩形;
(2)根据旋转的性质和三角函数解答即可.
解答 解:(1)∵点Q(1,2)倾斜60°运动后的对应点Q',过Q'作Q'E⊥OA,如图1,
∴AQ'=AQ,∠QAQ'=60°,
∴△QAQ'是等边三角形,
∴Q'E=$\frac{1}{2}AQ'$=1,AE=$\sqrt{3}$Q'E=$\sqrt{3}$,
∴Q'的纵坐标是1,横坐标是1+$\sqrt{3}$,
故答案为:$(1+\sqrt{3},1)$;
(2)因为平行于x轴的线段MN倾斜α运动后得到对应线段M′N′,如图2,
所以可得M′N′与MN平行且相等,
∵MN与x轴构成的四边形是矩形,
∴M′N′与x轴构成的四边形是平行四边形,
∴M′N′与MN平行且相等;
应用:(1)正方形AOBC倾斜α运动后,其各边中点E,F,G,H的对应点E′,F′,G′,H′构成的四边形是矩形;故答案为:矩形;
(2)设AB的中点为D,D点坐标为(1,2),
则CD∥x轴,且CD=2,
D点对应点D'为A'B'中点,
且C'D'=2,
而$C'D'=\frac{1}{2}A'B'$,
则A'B'=4=OA',
易得$∠α=\frac{1}{2}∠OA'B'$,
∴$cosα=\frac{{\sqrt{15}}}{4}$.
点评 此题主要考查了几何变换综合题,关键是根据旋转的性质,掌握旋转后对应线段相等分析.


科目:初中数学 来源: 题型:填空题
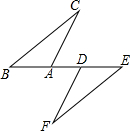 如图,点B、A、D、E在同一直线上,BD=AE,BC∥EF,要使△ABC≌△DEF,则只需添加一个适当的条件是BC=EF或∠BAC=∠EDF.(只填一个即可)
如图,点B、A、D、E在同一直线上,BD=AE,BC∥EF,要使△ABC≌△DEF,则只需添加一个适当的条件是BC=EF或∠BAC=∠EDF.(只填一个即可)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,已知△ABC的三个顶点的坐标分别为A(-2,3),B(-6,0),C(-1,0).
如图所示,已知△ABC的三个顶点的坐标分别为A(-2,3),B(-6,0),C(-1,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
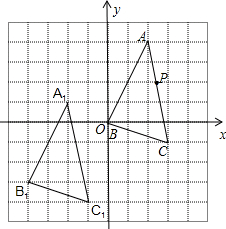 在如图所示的单位正方形网格中,△ABC经过平移后得到△A1B1C1,已知在AC上一点P(2.4,2)平移后的对应点为P1.
在如图所示的单位正方形网格中,△ABC经过平移后得到△A1B1C1,已知在AC上一点P(2.4,2)平移后的对应点为P1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
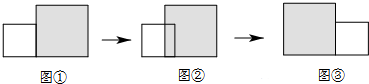
| A. | 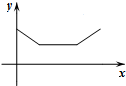 | B. | 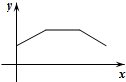 | C. | 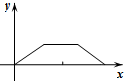 | D. | 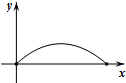 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com