
°æƒø°ø£®Œ Â∑¢œ÷£©
£®1£©»ÁÕº£®1£©Àƒ±þ–ŒABCD÷–£¨»ÙAB=AD£¨CB=CD£¨‘Úœþ∂ŒBD£¨ACµƒŒª÷√πÿœµŒ™°° °°£ª
£®Õÿ’πÃΩæø£©
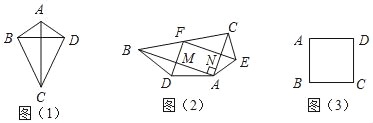
£®2£©»ÁÕº£®2£©‘⁄Rt°˜ABC÷–£¨µ„FŒ™–±±þBCµƒ÷–µ„£¨∑÷±“‘AB£¨ACŒ™µ◊±þ£¨‘⁄Rt°˜ABCÕ‚≤ø◊˜µ»—¸»˝Ω«–ŒABD∫Õµ»—¸»˝Ω«–ŒACE£¨¡¨Ω”FD£¨FE£¨∑÷±ΩªAB£¨AC”⁄µ„M£¨N£Æ ‘≤¬œÎÀƒ±þ–ŒFMANµƒ–Œ◊¥£¨≤¢Àµ√˜¿Ì”…£ª
£®Ω‚戌 £©
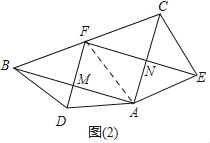
£®3£©»ÁÕº£®3£©‘⁄’˝∑Ω–ŒABCD÷–£¨AB=2![]() £¨“‘µ„AŒ™–˝◊™÷––ƒΩ´’˝∑Ω–ŒABCD–˝◊™60°„£¨µ√µΩ’˝∑Ω–ŒAB'C'D'£¨«Î÷±Ω”–¥≥ˆBD'∆Ω∑Ωµƒ÷µ£Æ
£¨“‘µ„AŒ™–˝◊™÷––ƒΩ´’˝∑Ω–ŒABCD–˝◊™60°„£¨µ√µΩ’˝∑Ω–ŒAB'C'D'£¨«Î÷±Ω”–¥≥ˆBD'∆Ω∑Ωµƒ÷µ£Æ
°æ¥∞∏°ø£®1£©AC¥π÷±∆Ω∑÷BD£ª£®2£©Àƒ±þ–ŒFMAN «æÿ–Œ£¨¿Ì”…º˚Ω‚Œˆ£ª£®3£©16+8![]() ªÚ16©Å8
ªÚ16©Å8![]()
°æΩ‚Œˆ°ø
£®1£©“¿æðµ„A‘⁄œþ∂ŒBDµƒ¥π÷±∆Ω∑÷œþ…œ£¨µ„C‘⁄œþ∂ŒBDµƒ¥π÷±∆Ω∑÷œþ…œ£¨º¥ø…µ√≥ˆAC¥π÷±∆Ω∑÷BD£ª
£®2£©∏˘æðRt°˜ABC÷–£¨µ„FŒ™–±±þBCµƒ÷–µ„£¨ø…µ√AF=CF=BF£¨‘Ÿ∏˘æðµ»—¸»˝Ω«–ŒABD ∫Õµ»—¸»˝Ω«–ŒACE£¨º¥ø…µ√µΩAD=DB£¨AE=CE£¨Ω¯∂¯µ√≥ˆ°œAMF=°œMAN=°œANF=90°„£¨º¥ø…≈–∂®Àƒ±þ–ŒAMFN «æÿ–Œ£ª
£®3£©∑÷¡Ω÷÷«Èøˆ£∫¢Ÿ“‘µ„AŒ™–˝◊™÷––ƒΩ´’˝∑Ω–ŒABCDƒÊ ±’Ζ˝◊™60°„£¨¢⁄“‘µ„AŒ™–˝◊™÷––ƒΩ´’˝∑Ω–ŒABCDÀ≥ ±’Ζ˝◊™60°„£¨∑÷±“¿æð–˝◊™µƒ–‘÷ “‘º∞π¥π…∂®¿Ì£¨º¥ø…µ√µΩΩ·¬€£Æ
£®1£©°þAB=AD£¨CB=CD£¨
°ýµ„A‘⁄œþ∂ŒBDµƒ¥π÷±∆Ω∑÷œþ…œ£¨µ„C‘⁄œþ∂ŒBDµƒ¥π÷±∆Ω∑÷œþ…œ£¨
°ýAC¥π÷±∆Ω∑÷BD£¨
π ¥∞∏Œ™£∫AC¥π÷±∆Ω∑÷BD£ª
£®2£©Àƒ±þ–ŒFMAN «æÿ–Œ£Æ¿Ì”…£∫
»ÁÕº2£¨¡¨Ω”AF£¨
°þRt°˜ABC÷–£¨µ„FŒ™–±±þBCµƒ÷–µ„£¨
°ýAF=CF=BF£¨
”÷°þµ»—¸»˝Ω«–ŒABD ∫Õµ»—¸»˝Ω«–ŒACE£¨
°ýAD=DB£¨AE=CE£¨
°ý”…£®1£©ø…µ√£¨DF°ÕAB£¨EF°ÕAC£¨
”÷°þ°œBAC=90°„£¨
°ý°œAMF=°œMAN=°œANF=90°„£¨
°ýÀƒ±þ–ŒAMFN «æÿ–Œ£ª
£®3£©BD°‰µƒ∆Ω∑ΩŒ™16+8![]() ªÚ16©Å8
ªÚ16©Å8![]() £Æ
£Æ
∑÷¡Ω÷÷«Èøˆ£∫
¢Ÿ“‘µ„AŒ™–˝◊™÷––ƒΩ´’˝∑Ω–ŒABCDƒÊ ±’Ζ˝◊™60°„£¨
»ÁÕºÀ˘ æ£∫π˝D'◊˜D'E°ÕAB£¨ΩªBAµƒ—”≥§œþ”⁄E£¨
”…–˝◊™ø…µ√£¨°œDAD'=60°„£¨
°ý°œEAD'=30°„£¨
°þAB=2![]() =AD'£¨
=AD'£¨
°ýD'E=![]() AD'=
AD'=![]() £¨AE=
£¨AE=![]() £¨
£¨
°ýBE=2![]() +
+![]() £¨
£¨
°ýRt°˜BD'E÷–£¨BD'2=D'E2+BE2=£®![]() £©2+£®2
£©2+£®2![]() +
+![]() £©2=16+8
£©2=16+8![]()
¢⁄“‘µ„AŒ™–˝◊™÷––ƒΩ´’˝∑Ω–ŒABCDÀ≥ ±’Ζ˝◊™60°„£¨
»ÁÕºÀ˘ æ£∫π˝B◊˜BF°ÕAD'”⁄F£¨

–˝◊™ø…µ√£¨°œDAD'=60°„£¨
°ý°œBAD'=30°„£¨
°þAB=2![]() =AD'£¨
=AD'£¨
°ýBF=![]() AB=
AB=![]() £¨AF=
£¨AF=![]() £¨
£¨
°ýD'F=2![]() ©Å
©Å![]() £¨
£¨
°ýRt°˜BD'F÷–£¨BD'2=BF2+D'F2=£®![]() £©2+£®2
£©2+£®2![]() -
-![]() £©2=16©Å8
£©2=16©Å8![]()
◊€…œÀ˘ ˆ£¨BD°‰∆Ω∑Ωµƒ≥§∂»Œ™16+8![]() ªÚ16©Å8
ªÚ16©Å8![]() £Æ
£Æ


 ◊÷¥ æ‰∂Œ∆™œµ¡–¥∞∏
◊÷¥ æ‰∂Œ∆™œµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥–£º∆ªÆ“ª¥Œ–‘π∫¬Ú≈≈«Ú∫Õ¿∫«Ú£¨√ø∏ˆ¿∫«Úµƒº€∏Ò±»≈≈«ÚπÛ30‘™£ªπ∫¬Ú2∏ˆ≈≈«Ú∫Õ3∏ˆ¿∫«Úπ≤–Ë340‘™£Æ
(1)«Û√ø∏ˆ≈≈«Ú∫Õ¿∫«Úµƒº€∏Ò£∫
(2)»Ù∏√–£“ª¥Œ–‘π∫¬Ú≈≈«Ú∫Õ¿∫«Úπ≤60∏ˆ£¨◊Ð∑—”√≤ª≥¨π˝3800‘™£¨«“π∫¬Ú≈≈«Úµƒ∏ˆ ˝…Ÿ”⁄39∏ˆ£Æ…Ë≈≈«Úµƒ∏ˆ ˝Œ™m£¨◊Ð∑—”√Œ™y‘™£Æ
¢Ÿ«Ûyπÿ”⁄mµƒ∫Ø ˝πÿœµ Ω£¨≤¢«Ûmø…»°µƒÀ˘”–÷µ£ª
¢⁄‘⁄—ß–£∞¥‘ı—˘µƒ∑Ω∞∏π∫¬Ú ±£¨∑—”√◊ÓµÕ£ø◊ÓµÕ∑—”√Œ™∂ý…Ÿ£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™£∫‘⁄∆Ω––Àƒ±þ–ŒABCD÷–£¨AM=CN.«Û÷§£∫Àƒ±þ–ŒMBND «∆Ω––Àƒ±þ–Œ.

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨º◊““¡Ω»À“‘œýÕ¨µƒ¬∑œþ«∞Õ˘æý¿Îµ•Œª![]() µƒ≈ý—µ÷––ƒ≤Œº”—ßœ∞£¨Õº÷–
µƒ≈ý—µ÷––ƒ≤Œº”—ßœ∞£¨Õº÷–![]() £¨
£¨![]() ∑÷±±Ì æº◊““¡Ω»À«∞Õ˘ƒøµƒµÿÀ˘◊þµƒ¬∑≥Ã
∑÷±±Ì æº◊““¡Ω»À«∞Õ˘ƒøµƒµÿÀ˘◊þµƒ¬∑≥Ã![]() («ß√◊)ÀÊ ±º‰
(«ß√◊)ÀÊ ±º‰![]() (∑÷)±‰ªØµƒ∫Ø ˝ÕºœÛ£¨“‘œ¬Àµ∑®£∫
(∑÷)±‰ªØµƒ∫Ø ˝ÕºœÛ£¨“‘œ¬Àµ∑®£∫
¢Ÿ““±»º◊÷«∞12∑÷÷”µΩ¥Ô
¢⁄º◊∆Ωæ˘ÀŸ∂»Œ™0.25«ß√◊/–° ±
¢€º◊°¢““œý”ˆ ±£¨““◊þ¡À6«ß√◊
¢Ð““≥ˆ∑¢6∑÷÷”∫Û◊∑…œº◊£¨∆‰÷–’˝»∑µƒ «(°°°°)
A.¢Ÿ¢⁄B.¢€¢ÐC.¢Ÿ¢€¢ÐD.¢⁄¢€¢Ð
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº1£¨≈◊ŒÔœþy=ax2+bx©Å2”Îx÷·Ωª”⁄µ„A£®©Å1£¨0£©£¨B£®4£¨0£©¡Ωµ„£¨”Îy÷·Ωª”⁄µ„C£¨æ≠π˝µ„Bµƒ÷±œþΩªy÷·”⁄µ„E£®0£¨2£©£Æ
£®1£©«Û∏√≈◊ŒÔœþµƒΩ‚Œˆ Ω£ª
£®2£©»ÁÕº2£¨π˝µ„A◊˜BEµƒ∆Ω––œþΩª≈◊ŒÔœþ”⁄¡Ì“ªµ„D£¨µ„P «≈◊ŒÔœþ…œŒª”⁄œþ∂ŒADœ¬∑Ωµƒ“ª∏ˆ∂ص„£¨¡¨Ω·PA£¨EA£¨ED£¨PD£¨«ÛÀƒ±þ–ŒEAPD√ʪ˝µƒ◊Ó¥Û÷µ£ª
£®3£©»ÁÕº3£¨¡¨Ω·AC£¨Ω´°˜AOC»∆µ„OƒÊ ±’Î∑ΩœÚ–˝◊™£¨º«–˝◊™÷–µƒ»˝Ω«–ŒŒ™°˜A°‰OC°‰£¨‘⁄–˝◊™π˝≥Ã÷–£¨÷±œþOC°‰”Î÷±œþBEΩª”⁄µ„Q£¨»Ù°˜BOQŒ™µ»—¸»˝Ω«–Œ£¨«Î÷±Ω”–¥≥ˆµ„Qµƒ◊¯±Í£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
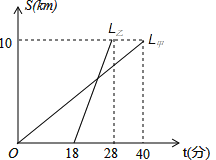
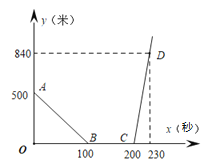
°æƒø°ø–°√˜∫լˬËø™≥µ»•÷–—Îπ´‘∞≤…∑Á£¨–°√˜∞÷∞÷∑¢œ÷À˚√«Õ¸º«¥¯ª≠± ∫Û¡¢º¥ø™≥µ◊∑∏œÀ˚√«.ºŸ…ˬˬË∫Õ∞÷∞÷µƒ≥µ‘⁄Õ¨“ª÷±œþπ´¬∑…œ‘»ÀŸ–– ª£¨µ±∞÷∞÷µƒ≥µ◊∑…œ¬Ë¬Ëµƒ≥µ∫Û£¨¡Ω≥µÕ£œ¬¿¥£¨∞÷∞÷∞—ª≠± Ωª∏¯–°√˜.»ª∫Û–°√˜∫լˬËø™≥µ“‘‘≠¿¥ÀŸ∂»µƒ![]() ±∂ºÃ–¯«∞––£¨∞÷∞÷‘Ú“‘¿¥ ±“ª∞εƒÀŸ∂»—ÿ‘≠¬∑ªÿº“£Æ…Ë–°√˜∞÷∞÷ø™≥µµƒ ±º‰Œ™
±∂ºÃ–¯«∞––£¨∞÷∞÷‘Ú“‘¿¥ ±“ª∞εƒÀŸ∂»—ÿ‘≠¬∑ªÿº“£Æ…Ë–°√˜∞÷∞÷ø™≥µµƒ ±º‰Œ™![]() £®√Σ©£¨¡Ω≥µº‰µƒæý¿ÎŒ™
£®√Σ©£¨¡Ω≥µº‰µƒæý¿ÎŒ™![]() £®√◊£©£¨
£®√◊£©£¨![]() πÿ”⁄
πÿ”⁄![]() µƒ≤ø∑÷∫Ø ˝πÿœµ»ÁÕºÀ˘ 棨µ±–°√˜∞÷∞÷ªÿµΩº“ ±£¨–°√˜∫լˬ˒˝∫√–– ª¡À»´≥õƒ
µƒ≤ø∑÷∫Ø ˝πÿœµ»ÁÕºÀ˘ 棨µ±–°√˜∞÷∞÷ªÿµΩº“ ±£¨–°√˜∫լˬ˒˝∫√–– ª¡À»´≥õƒ![]() £¨‘Ú–°√˜º“¿Î÷–—Îπ´‘∞µƒæý¿ÎŒ™________√◊
£¨‘Ú–°√˜º“¿Î÷–—Îπ´‘∞µƒæý¿ÎŒ™________√◊
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
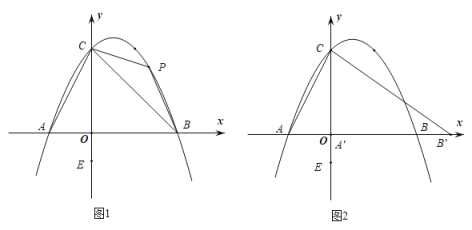
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨≈◊ŒÔœþ![]() ”Î
”Î![]() ÷·Ωª”⁄
÷·Ωª”⁄![]() °¢
°¢![]() ¡Ωµ„£¨Ωª
¡Ωµ„£¨Ωª![]() ÷·”⁄µ„
÷·”⁄µ„![]() £¨µ„
£¨µ„![]() πÿ”⁄≈◊ŒÔœþ∂‘≥∆÷·µƒ∂‘≥∆µ„Œ™µ„
πÿ”⁄≈◊ŒÔœþ∂‘≥∆÷·µƒ∂‘≥∆µ„Œ™µ„![]() .
.
£®1£©«Ûœþ∂Œ![]() µƒ≥§∂»£ª
µƒ≥§∂»£ª
£®2£©![]() Œ™œþ∂Œ
Œ™œþ∂Œ![]() …œ∑Ω≈◊ŒÔœþ…œµƒ»Œ“‚“ªµ„£¨µ„
…œ∑Ω≈◊ŒÔœþ…œµƒ»Œ“‚“ªµ„£¨µ„![]() Œ™
Œ™![]() £¨“ª∂ص„
£¨“ª∂ص„![]() ¥”µ„
¥”µ„![]() ≥ˆ∑¢‘À∂صΩ
≥ˆ∑¢‘À∂صΩ![]() ÷·…œµƒµ„
÷·…œµƒµ„![]() £¨‘Ÿ—ÿ
£¨‘Ÿ—ÿ![]() ÷·‘À∂ØµΩµ„
÷·‘À∂ØµΩµ„![]() .µ±Àƒ±þ–Œ
.µ±Àƒ±þ–Œ![]() µƒ√ʪ˝◊Ó¥Û ±£¨«Û
µƒ√ʪ˝◊Ó¥Û ±£¨«Û![]() µƒ◊Ó–°÷µ£ª
µƒ◊Ó–°÷µ£ª
£®3£©Ω´œþ∂Œ![]() —ÿ
—ÿ![]() ÷·œÚ”“∆Ω“∆£¨…Ë∆Ω“∆∫Ûµƒœþ∂ŒŒ™
÷·œÚ”“∆Ω“∆£¨…Ë∆Ω“∆∫Ûµƒœþ∂ŒŒ™![]() £¨÷±÷¡
£¨÷±÷¡![]() ∆Ω––”⁄
∆Ω––”⁄![]() ÷·£®µ„
÷·£®µ„![]() Œ™µ⁄2–°Œ ÷–∑˚∫œÃ‚“‚µƒ
Œ™µ⁄2–°Œ ÷–∑˚∫œÃ‚“‚µƒ![]() µ„£©£¨¡¨Ω”÷±œþ
µ„£©£¨¡¨Ω”÷±œþ![]() .Ω´
.Ω´![]() »∆◊≈
»∆◊≈![]() –˝◊™£¨…Ë–˝◊™∫Û
–˝◊™£¨…Ë–˝◊™∫Û![]() °¢
°¢![]() µƒ∂‘”¶µ„∑÷±Œ™
µƒ∂‘”¶µ„∑÷±Œ™![]() °¢
°¢![]() £¨‘⁄–˝◊™π˝≥Ã÷–÷±œþ
£¨‘⁄–˝◊™π˝≥Ã÷–÷±œþ![]() ”Î
”Î![]() ÷·Ωª”⁄µ„
÷·Ωª”⁄µ„![]() £¨”Îœþ∂Œ
£¨”Îœþ∂Œ![]() Ωª”⁄µ„
Ωª”⁄µ„![]() .µ±
.µ±![]() «“‘
«“‘![]() Œ™—¸µƒµ»—¸»˝Ω«–Œ ±£¨–¥≥ˆ
Œ™—¸µƒµ»—¸»˝Ω«–Œ ±£¨–¥≥ˆ![]() µƒ≥§∂».
µƒ≥§∂».
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥ ˝—ß¿œ ¶Œ™¡À¡ÀΩ‚—ß…˙‘⁄ ˝—ß—ßœ∞÷–≥£º˚¥ÌŒÛµƒæ¿’˝«Èøˆ£¨ ’ºØ’˚¿Ì¡À—ß…˙‘⁄◊˜“µ∫Õøº ‘÷–µƒ≥£º˚¥ÌŒÛ£¨±ý÷∆¡À10µ¿—°‘Ò£¨√øÂ3∑÷£¨∂‘À˚À˘Ωõƒ≥ı»˝£®1£©∞ý°¢£®2£©∞ýΩ¯––¡ÀºÏ≤‚£¨»ÁÕº±Ì 楔¡Ω∞ý∏˜Àʪ˙≥È»°µƒ10√˚—ß…˙µƒµ√∑÷«Èøˆ.
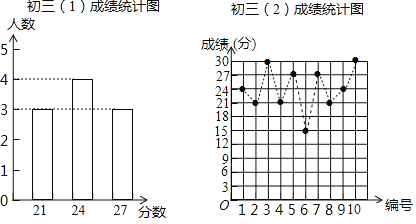
£®1£©¿˚”√Õº÷–Ã·π©µƒ–≈œ¢£¨≤π»´œ¬±Ì£∫
∞ýº∂ | ∆Ωæ˘ ˝/∑÷ | ÷–Œª ˝/∑÷ | ÷⁄ ˝/∑÷ |
≥ı»˝£®1£©∞ý | __________ | 24 | ________ |
≥ı»˝£®2£©∞ý | 24 | _________ | 21 |
£®2£©»Ù∞—24∑÷“‘…œ£®∫¨24∑÷£©º«Œ™°∞”≈–„°±£¨¡Ω∞ý∏˜40√˚—ß…˙£¨«Îπ¿º∆¡Ω∞ý∏˜”–∂ý…Ÿ√˚—ß…˙≥…º®”≈–„£ª
£®3£©π€≤Ï…œÕºµƒ ˝æð∑÷≤º«Èøˆ£¨«ÎÕ®π˝º∆À„Àµ√˜ƒƒ∏ˆ∞ýµƒ—ß…˙濥̵ƒµ√∑÷∏¸Œ»∂®£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
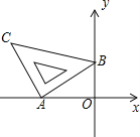
°æƒø°ø∫¨45°„Ω«µƒ÷±Ω«»˝Ω«∞»ÁÕº∑≈÷√‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨∆‰÷–A£®-3£¨0£©£¨B£®0£¨2£©£¨‘Ú÷±œþBCµƒΩ‚Œˆ ΩŒ™______£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com