
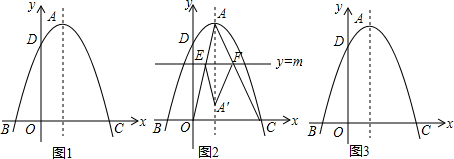
分析 (1)告诉了抛物线与x轴的两个交点坐标,因此将抛物线解析式设交点式,再将D点坐标代入即可求出解析式,将解析式配成顶点式即可得A点坐标;
(2)①利用△AEF∽△AOC,列出线段比例即可表示出EF;
②分两种情况:第一种,2≤m<4时,重叠部分的面积就是△AEF的面积,直接求△AEF的面积即可;第二种,0<m<2时,重叠部分的面积是一个梯形,同样根据相似,先表示出梯形的上底,再直接用梯形面积公式求出即可;
(3)先求出点A关于直线BD的对称点P,连接CP与BD的交点即为满足要求的点.
解答 解:(1)设抛物线的解析式为:y=a(x+1)(x-3),
将D(0,3)代入解析式得:3=-3a,
∴a=-1,
∴抛物线的解析式为:y=-(x+1)(x-3)=-x2+2x+3=-(x-1)2+4,
∴A(1,4).
(2)①由△AEF∽△AOC可得:$\frac{4-m}{4}=\frac{EF}{OC}$,
即:$\frac{4-m}{4}=\frac{EF}{3}$,
∴EF=$\frac{3}{4}(4-m)$.
②当2≤m<4时,重叠部分的面积就是△AEF的面积,
${S=S}_{△AEF}=\frac{1}{2}×EF×(4-m)$=$\frac{1}{2}×\frac{3}{4}(4-m)×(4-m)=\frac{3}{8}(m-4)^{2}$;
当0<m<2时,如下图所示:
A'E与x轴交于点G,A'F与x轴交于点H,
$\frac{GH}{EF}=\frac{2(4-m)-4}{4-m}$,
∴GH=3-$\frac{3}{2}m$,
$S={S}_{EFHG}=\frac{1}{2}×(EF+GH)×m$=$-\frac{9}{8}{m}^{2}$+3m,
综上所述:$S=\left\{\begin{array}{l}{-\frac{9}{8}{m}^{2}+3m(0<m<2)}\\{\frac{3}{8}{(m-4)}^{2}(2≤m<4)}\end{array}\right.$.
(3)如下图,
直线的BD的解析式为y=3x+3,
设P点为A点关于直线BD的对称点,
则直线PA的解析式为y=-$\frac{1}{3}$x+$\frac{13}{3}$,
设PA与BD交于点N,
将直线PA与BD的解析式联立可解得N($\frac{2}{5}$,$\frac{21}{5}$),
设P(t,-$\frac{1}{3}$t+$\frac{13}{3}$),
则t+1=$\frac{2}{5}×2$,
∴t=-$\frac{1}{5}$,
∴P(-$\frac{1}{5}$,$\frac{22}{5}$),
∴PC的解析式为:$y=-\frac{11}{8}x+\frac{33}{8}$,
联立PC与BD与的解析式可解得:M($\frac{9}{35}$,$\frac{132}{35}$).
点评 本题考查了待定系数法求抛物线解析式、相似三角形的判定与性质、翻折变换、重叠面积的计算、待定系数法求一次函数解析式、两直线相互垂直的性质、关于某条直线的对称点的坐标求法,最短路径问题等众多知识点,综合性非常强,难度较大.第(2)问求重叠面积的关键在于找准重叠部分的形状;第(3)问的关键在于找到A点关于BD的对称点.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
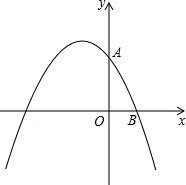 如图,已知点A(0,4)和点B(3,0)都在抛物线y=mx2+2mx+n上.
如图,已知点A(0,4)和点B(3,0)都在抛物线y=mx2+2mx+n上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
| 人数变化 | +0.6 | +0.4 | +0.2 | -0.5 | -0.8 | +0.2 | -0.3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com