【题目】如图，大刚在晚上由灯柱A走向灯柱B，当他走到M点时，发觉他身后影子的顶部刚好接触到灯柱A的底部，当他向前再走12米到N点时，发觉他身前的影子刚好接触到灯柱B的底部，已知大刚的身高是1.6米，两根灯柱的高度都是9.6米，设AM=NB=x米．求：两根灯柱之间的距离．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】(1)已知
，求
的最小值.
爱思考的小思想到了一种方法：先用
表示
得：
_____；
再把代入得到：
______；
再利用配方法得到：
(
_____)
+______；
根据完全平方式的非负性，就得到了的最小值是______.
请你补充完成小思的解答过程：
(2)根据小思的方法，请你求出：当
时，求出
的最小值.
(3)但是假如变成
，求
的最小值的时候小思的方法就不好用了，因此喜欢面对挑战的小喻同学想到了一种叫增量代换法：
设
，
，
，
，
∵，
∴
，
则
，
，
.
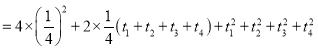故的最小值是
.
参考小喻的方法，当
时，
求出
的最小值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在Rt△ABC中，∠B＝90°，AB＝3，BC＝4，将△ABC折叠，使点B恰好落在斜边AC上，与点B′重合，AD为折痕，则DB＝_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在进行二次根式化简时，我们有时会碰上如
，
，
一样的式子，这样的式子我们可以将其进一步化简＝
，
，
以上这种化简的方法叫做分母有理化，请利用分母有理化解答下列问题：
（1）化简：
；
（2）若a是
的小数部分，求
的值；
（3）矩形的面积为3
+1，一边长为﹣2，求它的周长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列说法不正确的是（ ）
A. 了解全市中学生对泰州“三个名城”含义的知晓度的情况，适合用抽样调查
B. 若甲组数据方差S甲2=0.39，乙组数据方差S乙2=0.27，则乙组数据比甲组数据稳定
C. 某种彩票中奖的概率是
，买100张该种彩票一定会中奖
D. 数据﹣1、1.5、2、2、4的中位数是2
查看答案和解析>>
科目：初中数学 来源： 题型：
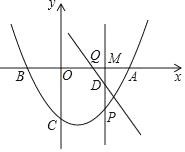
【题目】二次函数y=
+bx+c与一次函数y=kx﹣3的图象都经过x轴上的点A（4，0）和y轴上点C（0，﹣3）．
（1）直接写出b，c，k的值，b= ，c= ，k= ；
（2）二次函数与x轴的另一个交点为B，点M（m，0）在线段AB上运动，过点M作x轴的垂线交直线AC于点D；交抛物线于点P．
①是否存在实数m，使△PCD为直角三角形．若存在、求出m的值；若不存在，请说明理由；
②当0＜m＜4时，过D作直线AC的垂线交x轴于点Q，求PD+DQ的最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为参加11月23日举行的丹东市“我爱诗词”中小学生诗词大赛决赛，某校每班选25名同学参加预选赛，成绩分别为A、B、C、D四个等级，其中相应等级的得分依次记为10分、9分、8分、7分，学校将八年级的一班和二班的成绩整理并绘制成如下统计图：
根据以上提供的信息解答下列问题
（1）请补全一班竞赛成绩统计图；
（2）请直接写出a、b、c、d的值；
班级 | 平均数（分） | 中位数（分） | 众数（分） |
一班 | a＝ | b＝ | 9 |
二班 | 8.76 | c＝ | d＝ |
（3）请从平均数和中位数两个方面对这两个班级的成绩进行分析．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
