练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
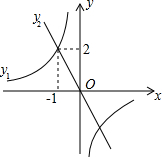
    如图，直线y1=k1x与双曲线y2=
    k2
    x
    的一个交点坐标是（-1，2）．由图象可知，当y1＞y2时，x的取值范围是（　　）
    A、x＜-1
    B、0＜x＜1
    C、x＜-1或0＜x＜1
    D、-1＜x＜0或x＞1
    考点：反比例函数与一次函数的交点问题
    专题：
    分析：先根据反比例函数的对称性求出反比例函数与正比例函数另一交点的坐标，再利用数形结合即可解答．
    解答：解：∵直线y1=k1x与双曲线y2=
    k2
    x
    的一个交点坐标是（-1，2），
    而反比例函数的图象关于原点对称，
    ∴反比例函数与正比例函数另一交点的坐标为（1，-2），
    由函数图象可知，当-1＜x＜0或x＞1时，y1在y2的上方，
    ∴当y1＞y2时x的取值范围是-1＜x＜0或x＞1．
    故选D．
    点评：本题考查的是反比例函数与一次函数的交点问题，解答此题的关键是利用数形结合求出x的取值范围．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    莘县旅游资源丰富，其中燕塔是莘县著名旅游景点（如图①）．一天身高1.5m的小明从A处仰视观看燕塔顶部，其仰角为30°．小明又向西走了30m，∠APB=15°（如图②）．请你帮小明算出雁塔的高度．（结果保留一位小数，参考数据：
    		2
    ≈1.41，
    		3
    ≈1.73）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，把长方形纸片ABCD沿EF折叠后，使得点D与点B重合，点C落在点C′的位置上．
    （1）折叠后，DC的对应线段是
     
    ，CF的对应线段是
     
    ；
    （2）若∠1=55°，求∠2、∠3的度数；
    （3）若AB=3，DE=4，求CF的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

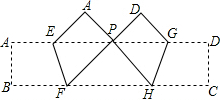    如图所示，折叠矩形纸条ABCD，使B，C两点落在AD边的P点处，折痕为EF，GH，若∠FPH的度数恰好为90°，PF=8，PH=6，则矩形ABCD的边BC的长为（　　）
    A、20B、22C、24D、30

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，点A在双曲线y=
    2
    x
    上，点B在双曲线y=
    5
    x
    上，且AB∥y轴，C、D在y轴上，若四边形ABCD为平行四边形，则它的面积为
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    市政府大力扶持节能环保产业，某企业研发出一种节能环保产品，获得市政府提供的120万元无息贷款，用于该产品的生产与销售，并约定用该产口的利润逐步偿还无息贷款，已知该产口的生产成本为每件60元，员工每人每月的工资为3000元，公司每月需支付其他费用15万元，该产品每月销售量y（万件）与销售单价x（元）之间的函数关系如图所示．
    （1）当60≤x≤80时，y与x之间的函数关系式是
     
    ；
         当80＜x＜120时，y与x之间的函数关系式是
     
    ；
    （2）当销售单价定为70元时，为保证公司每月利润达到6万元（利润=销售额-生产成本-员工工资-其他费用），该公司安排员工多少人？
    （3）若该公司有50名员工，则该公司最快可在几个月后还清无息贷款？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    武汉市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销，经过调查得到如下数据：
    销售单价x（元/件）…2030405060…
    每天销售量y（件）…500400300200100…
    （1）猜想y与x的函数关系，并求出函数关系；
    （2）当销售单价为多少时，工艺厂试销该工艺品每天获得的利润最大？最大利润是多少？（利润=销售总价-成本总价）；
    （3）武汉市物价部门规定，该工艺品销售单价最高不能超过35元/件，若此工艺厂要求该产品利润最低为5000元，那么销售单价的范围为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，边长为1的小正方形构成的网格中，半径为1的⊙O的圆心O在格点上，则∠AED的正弦值等于（　　）
    A、
    		5
    5
    B、
    2
    		5
    5
    C、2
    D、
    1
    2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    		3x-6
    若在实数范围内有意义，则x的取值范围是（　　）
    A、x≥-1B、x≠-2
    C、x≥2D、x≠2

    查看答案和解析>>

    同步练习册答案