
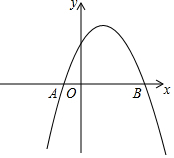
 如图,已知抛物线y=-x2+bx+c经过A(-1,0),B(3,0)两点.
如图,已知抛物线y=-x2+bx+c经过A(-1,0),B(3,0)两点.分析 (1)将A与B的坐标代入抛物线的解析式即可求出b与c的值.
(2)根据图象即可求出y的取值范围.
(3)设P(x,y),△PAB的高为|y|,AB=4,由S△PAB=10列出方程即可求出y的值,从而可求出P的坐标.
解答 解:(1)将A(-1,0)和B(3,0)代入y=-x2+bx+c
∴$\left\{\begin{array}{l}{0=-1-b+c}\\{0=-9+3b+c}\end{array}\right.$
解得:$\left\{\begin{array}{l}{b=2}\\{c=3}\end{array}\right.$
∴抛物线的解析式为:y=-x2+2x+3
∴顶点坐标为:(1,4)
(2)由于抛物线的对称轴为:x=1,
∴0<x<3时,
∴0<y≤4
(3)设P(x,y)
∴△PAB的高为|y|,
∵A(-1,0)、B(3,0)
∴AB=4
∵S△PAB=10,
∴$\frac{1}{2}$×4×|y|=10
∴y=±5,
当y=5时,
∴5=-x2+2x+3
此时方程无解,
当y=-5时,
∴-5=-x2+2x+3,
解得:x=4或x=-2,
∴P(4,-5)或(-2,-5)
点评 本题考查二次函数的综合问题,涉及待定系数法求解析式,二次函数图象的性质,解方程等知识,属于中等题型.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 为了审核书稿中的错别字,选择抽样调查 | |
| B. | 为了了解春节联欢晚会的收视率,选择全面调查 | |
| C. | “射击运动员射击一次,命中靶心”是随机事件 | |
| D. | “366人中至少有2人的生日是同月同日”是必然事件 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | y=-2x2 | B. | y=2x2 | C. | y=-0.5x2 | D. | y=0.5x2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x=2}\\{y=-3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=3}\\{y=-5}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=1}\\{y=-5}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,四边形ABCD的对角线AC,BD相交于点O,且AB∥CD,添加下列条件后仍不能判断四边形ABCD是平行四边形的是( )
如图,四边形ABCD的对角线AC,BD相交于点O,且AB∥CD,添加下列条件后仍不能判断四边形ABCD是平行四边形的是( )| A. | AB=CD | B. | AD∥BC | C. | OA=OC | D. | AD=BC |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com