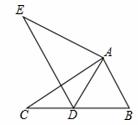
如图，在△ABC中，AB=2，BC=3．6，∠B=60°，将△ABC绕点A按顺时针旋转一定角度得到△ADE，当点B的对应点D恰好落在BC边上时，则CD的长为 ．
科目：初中数学 来源： 题型：
一次函数y=(k-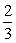
)x－3k+10（k为偶数）的图象经过第一、二、三象限，与x轴、y轴分别交于A、B两点，过点B作一直线与坐标轴围成的三角形面积为2，交x轴于点C.
（1）求k的值；
（2）若一抛物线经过点A、B、C三点，求此抛物线的解析式。
（3）当抛物线开口向上时过A、B、C三点作△ABC，求tan∠ABC的值。
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，等腰梯形ABCD中，AB∥CD，AB＝
， CD＝
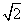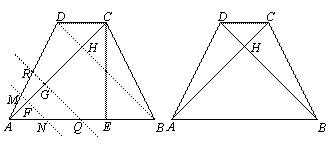
，高CE＝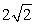
，对角线AC、BD交于点H．平行于线段BD的两条直线MN、RQ同时从点A出发，沿AC方向向点C匀速平移，分别交等腰梯形ABCD的边于M、N和R、Q，分别交对角线AC于F、G，当直线RQ到达点C时，两直线同时停止移动．记等腰梯形ABCD被直线MN扫过的面积为
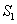，被直线RQ扫过的面积为
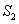，若直线MN平移的速度为1单位/秒，直线RQ平移的速度为2单位/秒，设两直线移动的时间为x秒．
（1）填空：∠AHB＝____________；AC＝_____________；
（2）若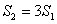
，求x．
 |
查看答案和解析>>
科目：初中数学 来源： 题型：
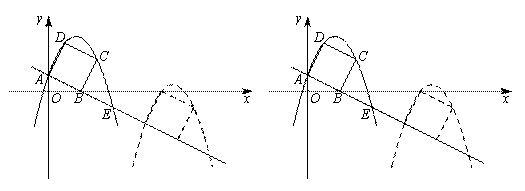
如图，已知直线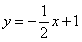
与坐标轴交于A，B两点，以线段AB为边向上作正方形ABCD，过点A，D，C的抛物线与直线的另一个交点为E．
（1）请直接写出C，D两点的坐标，并求出抛物线的解析式；
（2）若正方形以每秒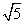
个单位长度的速度沿射线AB下滑，直至顶点D落在x轴上时停止，设正方形落在x轴下方部分的面积为S，求S关于滑行时间t的函数关系式，并写出相应自变量t的取值范围；
（3）在（2）的条件下，抛物线与正方形一起平移，同时停止，求抛物线上C，E两点间的抛物线弧所扫过的面积．
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，那么（ ）
B、
C、 
D、
cm C．
cm D．
cm
．
为第行第
列的数，如
=4，那么
是 。