
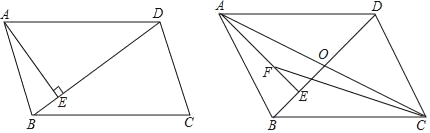
【题目】如图,在平行四边形ABCD中,AE⊥BD于E.
(1)若BC=BD,![]() ,AD=15,求△ABD的周长.
,AD=15,求△ABD的周长.
(2)若∠DBC=45°,对角线AC、BD交于点O,F为AE上一点,且AF=2EO,求证:CF=![]() AB.
AB.
【答案】(1)![]() ;(2)详见解析
;(2)详见解析
【解析】
(1)根据平行四边形的性质可推出AD=BD=15,然后设BE=x,则AB=![]() x,DE=BD﹣BE=15﹣x,利用勾股定理建立方程求出x,即可求周长;
x,DE=BD﹣BE=15﹣x,利用勾股定理建立方程求出x,即可求周长;
(2)延长AE与BC交于点M,过点O作OG∥AE,分别交BC、CF于点G、H,连接EH,BF,并延长BF,与AD交于点N,连接DF,DG,首先通过平行四边形的性质推导OH是△ACF的中位线,再判定四边形BGDN是正方形,最后证明△DNF≌△DGC即可得出结论.
(1)解:∵四边形ABCD是平行四边形,
∴AD=BC,
∵BC=BD,
∴AD=BD=15,
∵![]() ,
,
设BE=x,则AB=![]() x,DE=BD﹣BE=15﹣x,
x,DE=BD﹣BE=15﹣x,
∴AE=![]() =
=![]() =3x,AE2+DE2=AD2,
=3x,AE2+DE2=AD2,
即:![]() ,
,
解得:x=3,
∴AB=3![]() ,
,
∴△ABD的周长=AD+BD+AB=15+15+3![]() =30+3
=30+3![]() ;
;
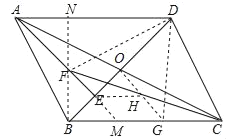
(2)证明:延长AE与BC交于点M,过点O作OG∥AE,分别交BC、CF于点G、H,连接EH,BF,并延长BF,与AD交于点N,连接DF,DG,如图所示:
∵AE⊥BD,
∴OG⊥BD,
∵四边形ABCD是平行四边形,
∴OB=OD,OA=OC,AB=CD,
∴BG=DG,
∵∠DBC=45°,
∴∠BDG=45°,
∴∠BGD=90°,
∵OG∥AM,OA=OC,
∴OH是△ACF的中位线,
∴OH=![]() AF=OE,HF=HC,
AF=OE,HF=HC,
∴∠OEH=∠OHE=45°=∠OBC,
∴EH∥BC,
∴EF=ME,
∵BE⊥MF,
∴BF=BM,
∴∠MBE=∠EBF=45°,
∴∠DNB=∠NBG=90°,
∴四边形BGDN是正方形,
∴DG=DN=BN=BG,
∴MG=FN,
∵AM∥OG,OA=OC,
∴MG=CG,
∴CG=FN,
在△DNF和△DGC中,
 ,
,
∴△DNF≌△DGC(SAS),
∴DF=DC,∠NDF=∠GDC,
∴∠FDC=∠NDG=90°,
∴CF=![]() CD,
CD,
∴CF=![]() AB.
AB.


科目:初中数学 来源: 题型:
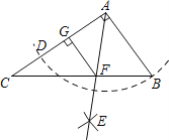
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=1,tanC=![]() ,以点A为圆心,AB长为半径作弧交AC于D,分别以B、D为圆心,以大于
,以点A为圆心,AB长为半径作弧交AC于D,分别以B、D为圆心,以大于![]() BD长为半径作弧,两弧交于点E,射线AE与BC于F,过点F作FG⊥AC于G,则FG的长为______.
BD长为半径作弧,两弧交于点E,射线AE与BC于F,过点F作FG⊥AC于G,则FG的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
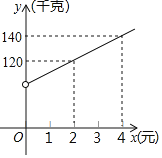
【题目】安顺市某商贸公司以每千克40元的价格购进一种干果,计划以每千克60元的价格销售,为了让顾客得到更大的实惠,现决定降价销售,已知这种干果销售量![]() (千克)与每千克降价
(千克)与每千克降价![]() (元)
(元)![]() 之间满足一次函数关系,其图象如图所示:
之间满足一次函数关系,其图象如图所示:
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)商贸公司要想获利2090元,则这种干果每千克应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,BC=4,⊙P与△ABC的边或边的延长线相切.若⊙P半径为2,△ABC的面积为5,则△ABC的周长为( )
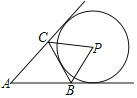
A.8B.10C.13D.14
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器超市销售每台进价分别为2000元、1700元的A、B两种型号的空调,如表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 18000元 |
第二周 | 4台 | 10台 | 31000元 |
(进价、售价均保持不变,利润=销售总收入进货成本)
(1)求A、B两种型号的空调的销售单价;
(2)若超市准备用不多于54000元的金额再采购这两种型号的空调共30台,求A种型号的空调最多能采购多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,港口A在观测站O的正东方向,OA=4.某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于x的不等式组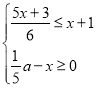 至少有3个整数解,且关于x的分式方程
至少有3个整数解,且关于x的分式方程![]() 的解为整数,则符合条件的所有整数a的取值之和为( )
的解为整数,则符合条件的所有整数a的取值之和为( )
A.﹣10B.﹣9C.﹣7D.﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
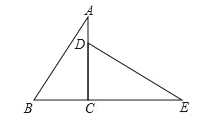
【题目】如图,在Rt△ABC中,∠ACB=90°,△DCE是△ABC绕着点C顺时针方向旋转得到的,此时B、C、E在同一直线上.
(1)旋转角的大小;
(2)若AB=10,AC=8,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
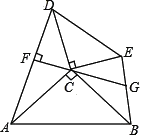
【题目】如图,点 C 为 Rt△ACB 与 Rt△DCE 的公共点,∠ACB=∠DCE=90°,连 接 AD、BE,过点 C 作 CF⊥AD 于点 F,延长 FC 交 BE 于点 G.若 AC=BC=25,CE=15, DC=20,则![]() 的值为___________.
的值为___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com