
【题目】如图,AB是大半圆O的直径,AO是小半圆M的直径,点P是大半圆O上一点,PA与小半圆M交于点C,过点C作CD⊥OP于点D. 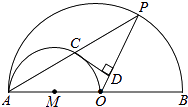
(1)求证:CD是小半圆M的切线;
(2)若AB=8,点P在大半圆O上运动(点P不与A,B两点重合),设PD=x,CD2=y. ①求y与x之间的函数关系式,并写出自变量x的取值范围;
②当y=3时,求P,M两点之间的距离.
【答案】
(1)解:连接CO、CM,如图1所示.
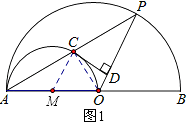
∵AO是小半圆M的直径,
∴∠ACO=90°即CO⊥AP.
∵OA=OP,
∴AC=PC.
∵AM=OM,
∴CM∥PO.
∴∠MCD=∠PDC.
∵CD⊥OP,
∴∠PDC=90°.
∴∠MCD=90°,即CD⊥CM.
∵CD经过半径CM的外端C,且CD⊥CM,
∴直线CD是小半圆M的切线
(2)解:①∵CO⊥AP,CD⊥OP,
∴∠OCP=∠ODC=∠CDP=90°.
∴∠OCD=90°﹣∠DCP=∠P.
∴△ODC∽△CDP.
∴ ![]() .
.
∴CD2=DPOD.
∵PD=x,CD2=y,OP= ![]() AB=4,
AB=4,
∴y=x(4﹣x)=﹣x2+4x.
当点P与点A重合时,x=0;当点P与点B重合时,x=4;
∵点P在大半圆O上运动(点P不与A,B两点重合),
∴0<x<4.
∴y与x之间的函数关系式为y=﹣x2+4x,
自变量x的取值范围是0<x<4.
②当y=3时,﹣x2+4x=3.
解得:x1=1,x2=3.
(i)当x=1时,如图2所示.
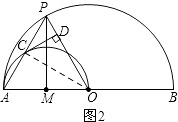
在Rt△CDP中,
∵PD=1,CD= ![]() .
.
∴tan∠CPD= ![]() =
= ![]() ,
,
∴∠CPD=60°.
∵OA=OP,
∴△OAP是等边三角形.
∵AM=OM,
∴PM⊥AO.
∴PM= ![]()
= ![]()
=2 ![]() .
.
(ii)当x=3时,如图3所示.

同理可得:∠CPD=30°.
∵OA=OP,
∴∠OAP=∠APO=30°.
∴∠POB=60°
过点P作PH⊥AB,垂足为H,连接PM,如图3所示.
∵sin∠POH= ![]() =
= ![]() =
= ![]() ,
,
∴PH=2 ![]() .
.
同理:OH=2.
在Rt△MHP中,
∵MH=4,PH=2 ![]() ,
,
∴PM= ![]()
= ![]()
=2 ![]() .
.
综上所述:当y=3时,P,M两点之间的距离为2 ![]() 或2
或2 ![]() .
.
【解析】(1)连接CO、CM,只需证到CD⊥CM.由于CD⊥OP,只需证到CM∥OP,只需证到CM是△AOP的中位线即可.(2)①易证△ODC∽△CDP,从而得到CD2=DPOD,进而得到y与x之间的函数关系式.由于当点P与点A重合时x=0,当点P与点B重合时x=4,点P在大半圆O上运动(点P不与A,B两点重合),因此自变量x的取值范围为0<x<4.②当y=3时,得到﹣x2+4x=3,求出x.根据x的值可求出CD、PD的值,从而求出∠CPD,运用勾股定理等知识就可求出P,M两点之间的距离.
【考点精析】解答此题的关键在于理解平行线的判定与性质的相关知识,掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质,以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


科目:初中数学 来源: 题型:
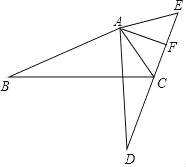
【题目】如图,∠BAD=∠CAE,AB=AD,AC=AE.且E,F,C,D在同一直线上.
(1)求证:△ABC≌△ADE;
(2)若∠B=30°,∠BAC=100°,点F是CE的中点,连结AF,求∠FAE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国“蛟龙”号深潜器目前最大深潜极限为7062.68米.某天该深潜器在海面下1800米的A点处作业(如图),测得正前方海底沉船C的俯角为45°,该深潜器在同一深度向正前方直线航行2000米到B点,此时测得海底沉船C的俯角为60°.
(1)沉船C是否在“蛟龙”号深潜极限范围内?并说明理由;
(2)由于海流原因,“蛟龙”号需在B点处马上上浮,若平均垂直上浮速度为2000米/时,求“蛟龙”号上浮回到海面的时间.(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E(与点B、C不重合)是BC边上一点,将线段EA绕点E顺时针旋转90°到EF,过点F作BC的垂线交BC的延长线于点G,连接CF.
(1)求证:△ABE≌△EGF;
(2)若AB=2,S△ABE=2S△ECF,求BE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是( )

A. 2 B. ![]() C.
C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
(材料)如图,对任意符合条件的直角三角形BAC,绕其锐角顶点逆时针旋转90°得△DAE,所以∠BAE=90°,且四边形ACFD是一个正方形,它的面积和四边形ABFE面积相等,而四边形ABFE面积等于Rt△BAE和Rt△BFE的面积之和,根据图形我们就能证明勾股定理: ![]() .
.

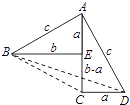
(请回答)如图是任意符合条件的两个全等的Rt△BEA和Rt△ACD拼成的,你能根据图示再写一种证明勾股定理的方法吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直线L上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1、2、3,正放置的四个正方形的面积依次是S1、S2、S3、S4 , 则S1+2S2+2S3+S4=()
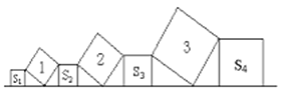
A. 5 B. 4 C. 6 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC与△A′B′C′都是等腰三角形,且AB=AC=5,A′B′=A′C′=3,若∠B+∠B′=90°,则△ABC与△A′B′C′的面积比为 . 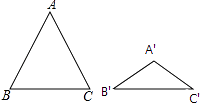
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 中,AB=AC,BD 平分∠ABC 交 AC 于 G,DM//BC 交∠ABC 的外角平分线于 M, 交 AB、AC 于 F、E,下列结论:①MB⊥BD;②FD=FB;③MD=2CE. 其中一定正确的有( )
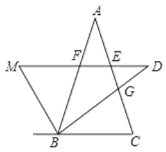
A. 0 个 B. 1 个 C. 2 个 D. 3 个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com