
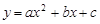 的图象与x轴交于(
的图象与x轴交于(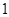 ,0)和(
,0)和(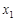 ,0),其中
,0),其中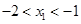 ,与
,与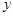 轴交于正半轴上一点.下列结论:①
轴交于正半轴上一点.下列结论:①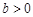 ;②
;②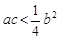 ;③
;③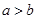 ;④
;④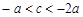 .其中所有正确结论的序号是_______.
.其中所有正确结论的序号是_______.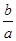 , x1·x2=
, x1·x2=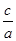 ,① x2="1>0," -2<x1<-1 ∴
,① x2="1>0," -2<x1<-1 ∴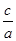 <0, -
<0, -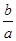 <0 又二次函数与y轴交于正半轴∴c>0 得a<0 b<0, ② ∵ac<
<0 又二次函数与y轴交于正半轴∴c>0 得a<0 b<0, ② ∵ac<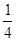 b2 图像与x轴有两个交点,4ac-b2>0 ∴ac<
b2 图像与x轴有两个交点,4ac-b2>0 ∴ac<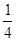 b2③∵x2="1" ∴a+b+c="0" ∴c="-a-b" ∴
b2③∵x2="1" ∴a+b+c="0" ∴c="-a-b" ∴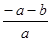 <0 -a-b>0即-a>b④ ∵a+b+c="0∴b=-a-c" 又-
<0 -a-b>0即-a>b④ ∵a+b+c="0∴b=-a-c" 又-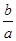 <0 ∴
<0 ∴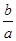 >0 即
>0 即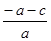 >0 ∴-a-c<0 ∴-a<c 根据韦达定理 X1 乘以X2 等于c/a ∵a﹤0 所以
>0 ∴-a-c<0 ∴-a<c 根据韦达定理 X1 乘以X2 等于c/a ∵a﹤0 所以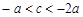 同时除以a变化为 –1﹤c/a﹤-2 又∵方程中x2=1 -2<x<1 ∴-2<x1x2<1
同时除以a变化为 –1﹤c/a﹤-2 又∵方程中x2=1 -2<x<1 ∴-2<x1x2<1

科目:初中数学 来源:不详 题型:解答题
 交y轴于点A.抛物线
交y轴于点A.抛物线 的图象过点E(-1,0),并与直线l相交于A、B两点.
的图象过点E(-1,0),并与直线l相交于A、B两点.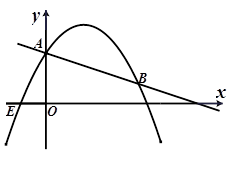
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 与
与 轴交于A、B两点,点C是AB的中点,CD⊥AB且CD=AB.直线BE与
轴交于A、B两点,点C是AB的中点,CD⊥AB且CD=AB.直线BE与 轴平行,点F是射线BE上的一个动点,连接AD、AF、DF.
轴平行,点F是射线BE上的一个动点,连接AD、AF、DF.
 ,
, ),AF=
),AF= .
. ,
, ,且AB的长为
,且AB的长为 ,其中
,其中 .如图2,当∠DAF=45时,求
.如图2,当∠DAF=45时,求 的值和∠DFA的正切值.
的值和∠DFA的正切值.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com