
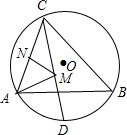
 如图,△ABC内接于半径为2的⊙O,其中∠ABC=45°,∠ACB=60°,CD平分∠ACB交⊙O于D,点M、N分别是线段CD、AC上的动点,求MA+MN的最小值.
如图,△ABC内接于半径为2的⊙O,其中∠ABC=45°,∠ACB=60°,CD平分∠ACB交⊙O于D,点M、N分别是线段CD、AC上的动点,求MA+MN的最小值. 解:连接OA,OC,
解:连接OA,OC,| 2OA2 |
| 2×4 |
| 2 |
| 2 |
| 2 |
| ||
| 2 |
| 6 |
| 6 |


科目:初中数学 来源: 题型:
 如图,在△ABC中,∠ACB=90°,AC=BC,AE是BC的中线,过点C作CF⊥AE于F,过B作BD⊥CB交CF的延长线于点D.
如图,在△ABC中,∠ACB=90°,AC=BC,AE是BC的中线,过点C作CF⊥AE于F,过B作BD⊥CB交CF的延长线于点D.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,抛物线y=-x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点A的坐标为(-1,0),与y轴交于点C(0,3),作直线BC.动点P在x轴上运动,过点P作PM⊥x轴,交抛物线于点M,交直线BC于点N,设点P的横坐标为m.
如图,抛物线y=-x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点A的坐标为(-1,0),与y轴交于点C(0,3),作直线BC.动点P在x轴上运动,过点P作PM⊥x轴,交抛物线于点M,交直线BC于点N,设点P的横坐标为m.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知直线y=
已知直线y=| 3 |
| 4 |
| 1 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、“明天降雨的概率是50%”表示明天有半天都在降雨 | ||||||||
| B、数据4,4,5,5,0的中位数和众数都是5 | ||||||||
| C、要了解一批钢化玻璃的最少允许碎片数,应采用普查的方式 | ||||||||
D、若甲、乙两组数中各有20个数据,平均数
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com