
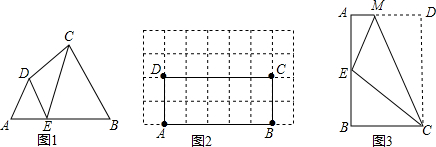
分析 (1)要证明点E是四边形ABCD的AB边上的相似点,只要证明有一组三角形相似就行,很容易证明△ADE∽△BEC,所以问题得解.
(2)根据两个直角三角形相似得到强相似点的两种情况即可.
(3)因为点E是梯形ABCD的AB边上的一个强相似点,所以就有相似三角形出现,根据相似三角形的对应线段成比例,可以判断出BE和BC的数量关系,再根据相似三角形的面积比等于相似比的平方从而可求出解.
解答 解:(1)点E是四边形ABCD的边AB上的相似点.
理由:∵∠A=55°,
∴∠ADE+∠DEA=125°.
∵∠DEC=55°,
∴∠BEC+∠DEA=125°.
∴∠ADE=∠BEC.(2分)
∵∠A=∠B,
∴△ADE∽△BEC.
∴点E是四边形ABCD的AB边上的相似点.
(2)作图如下: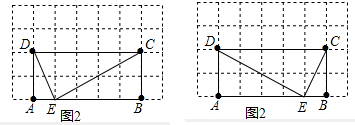
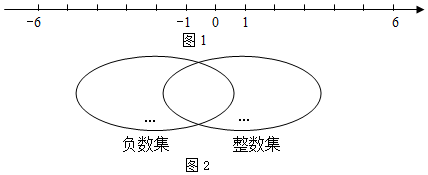
(3)∵点E是四边形ABCM的边AB上的一个强相似点,
∴△AEM∽△BCE∽△ECM,
∴∠BCE=∠ECM=∠AEM.
由折叠可知:△ECM≌△DCM,
∴∠ECM=∠DCM,CE=CD,
∴∠BCE=$\frac{1}{2}$∠BCD=30°,
∴BE=$\frac{1}{2}$CE=$\frac{1}{2}$AB.
在Rt△BCE中,tan∠BCE=$\frac{BE}{BC}$=tan30°,
∴$\frac{BE}{BC}$=$\frac{\sqrt{3}}{3}$,
∴S△AME:S△MEC=1:3,
故答案为:1:3.
点评 本题是相似三角形综合题,主要考查了相似三角形的对应边成比例的性质,读懂题目信息,理解强相似点的定义是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 -4,|-2|,-2,-(-3.5),0,-1$\frac{1}{2}$
-4,|-2|,-2,-(-3.5),0,-1$\frac{1}{2}$查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 姓名 | 小明 | 小彬 | 小丽 | 小亮 | 小颖 | 小山 |
| 身高 | 159 | 161 | 160 | 152 | 162 | 168 |
| 身高与平均身高的差 | -1 | +1 | 0 | -8 | +2 | +8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com