
【题目】在菱形ABCD中,∠BAD=α,E为对角线AC上的一点(不与A,C重合)将射线EB绕点E顺时针旋转β角之后,所得射线与直线AD交于F点.试探究线段EB与EF的数量关系.
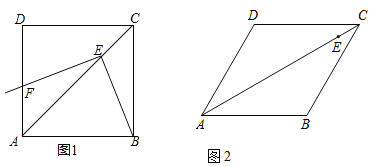
(1)如图1,当α=β=90°时,EB与EF的数量关系为 ;
(2)如图2,当α=60°,β=120°时,
①依题意补全图形;
②探究(1)的结论是否成立,若成立,请给出证明;若不成立,请举出反例证明.
【答案】(1)EB=EF;(2)①见解析;②成立,理由见解析
【解析】
(1)作EM⊥AD于M,EN⊥AB于N.根据角平分线的性质可证EM=EN,从而根据“ASA”可证△EMF≌△ENB,由全等三角形对应边相等得到EB=EF;
(2)①依题意以E为旋转中心,在EB顺时针方向作∠BEF=120°,与AD的延长线交于F.
②方法一:过点E作EM⊥AF于M,EN⊥AB于N,利用菱形的性质得出,∠DAC=∠BAC,再用角平分线的性质,得出EM=EN,进而证明△EFM≌△EBN即可证明EF=EB;
方法二:连接ED,利用菱形的性质可证明△AED≌△AEB,所以ED=EB,∠ADE=∠ABE,再证明∠F=∠FDE,根据等角对等边EF=ED,即可证明EF=EB.
(1)EB=EF,
理由是:如图1,作EM⊥AD于M,EN⊥AB于N.
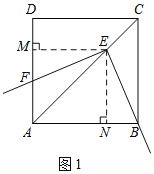
∵四边形ABCD是菱形,且∠BAD=90°,
∴菱形ABCD是正方形,
∴AE平分∠DAB,
∴EM=EN,
∵∠BEF=∠NEM=90°,
∴∠MEF=∠NEB,
∵∠EMF=∠BNE=90°,
∴△EMF≌△ENB(ASA),
∴EB=EF;
故答案为:EB=EF;
(2)①补全图形如图2所示,
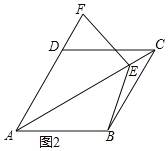
②结论依然成立EB=EF;
证法1:如图3,
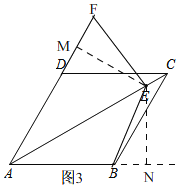
过点E作EM⊥AF于M,EN⊥AB于N.
∵四边形ABCD为菱形,
∴∠CAD=∠CAB.
∵EM⊥AF,EN⊥AB.
∴∠FME=∠ENB=90°,EM=EN,
∵∠BAD=60°,∠BEF=120°,
∴∠F+∠ABE=360°﹣∠BAD﹣∠BEF=180°.
∵∠ABE+∠EBN=180°,
∴∠F=∠EBN;
在△EFM与△EBN中,
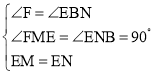
∴△EFM≌△EBN(AAS).
∴EF=EB;
证法2:如图4,连接ED
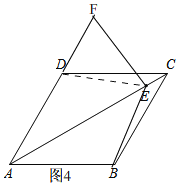
∵四边形ABCD是菱形,
∴AD=AB,∠DAC=∠BAE.
又∵AE=AE,
∴△ADE≌△ABE(SAS).
∴ED=EB,∠ADE=∠ABE,
又∵∠DAB=60°,∠BEF=120°.
∴∠F+∠ABE=180°.
又∵∠ADE+∠FDE=180°,
∴∠F=∠FDE.
∴EF=ED.
∴EF=EB.


科目:初中数学 来源: 题型:
【题目】在正方形 ABCD 中,M 是 BC 边上一点,且点 M 不与 B、C 重合,点 P 在射线 AM 上,将线段 AP 绕点 A 顺时针旋转 90°得到线段 AQ,连接BP,DQ.
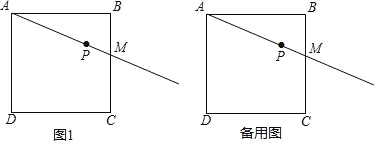
(1)依题意补全图 1;
(2)①连接 DP,若点 P,Q,D 恰好在同一条直线上,求证:DP2+DQ2=2AB2;
②若点 P,Q,C 恰好在同一条直线上,则 BP 与 AB 的数量关系为: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】红红和娜娜按下图所示的规则玩“锤子、剪刀、布”游戏,
游戏规则:若一人出“剪刀”,另一人出“布”,则出“剪刀”者胜;若一人出“锤子”,另一人出“剪刀”,则出“锤子”者胜;若一人出“布”,另一人出“锤子”,则出“布”者胜,若两人出相同的手势,则两人平局.
下列说法中错误的是
A. 红红不是胜就是输,所以红红胜的概率为![]()
B. 红红胜或娜娜胜的概率相等
C. 两人出相同手势的概率为![]()
D. 娜娜胜的概率和两人出相同手势的概率一样
查看答案和解析>>
科目:初中数学 来源: 题型:
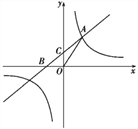
【题目】如图15,直线y=x+b与双曲线y=![]() 都经过点A(2,3),直线y=x+b与x轴、y轴分别交于B、C两点.
都经过点A(2,3),直线y=x+b与x轴、y轴分别交于B、C两点.
(1)求直线和双曲线的函数关系式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四张形状相同的卡片如图所示,将卡片洗匀后背面朝上放置在桌面上,小明先随机抽一张卡片,记下数字为![]() 后放回,小亮再随机抽一张卡片,记下数字为
后放回,小亮再随机抽一张卡片,记下数字为![]() .两人在此基础上共同协商一个游戏规则:当
.两人在此基础上共同协商一个游戏规则:当![]() 时小明获胜,否则小亮获胜,问他们规定的游戏规则公平吗?请说明理由.
时小明获胜,否则小亮获胜,问他们规定的游戏规则公平吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ABC=90°,∠BAC=30°,将△ABC绕点A顺时针旋转一定的角度![]() 得到△AED,点B、C的对应点分别是E、D.
得到△AED,点B、C的对应点分别是E、D.
(1)如图1,当点E恰好在AC上时,求∠CDE的度数;
(2)如图2,若![]() =60°时,点F是边AC中点,求证:四边形BFDE是平行四边形.
=60°时,点F是边AC中点,求证:四边形BFDE是平行四边形.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知抛物线y=![]() x2+bx+c经过点A(-1,0),B(5,0).
x2+bx+c经过点A(-1,0),B(5,0).

(1)求抛物线的解析式并写出顶点M的坐标;
(2)若点C在抛物线上,且点C的横坐标为8,求四边形AMBC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C为半径OA的上的中点,CD⊥AB交⊙O于点D和点E,DF∥AB交⊙O于F,连结AF,AD.
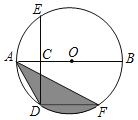
(1)求∠DAF的度数;
(2)若AB=10,求弦AD,AF和![]() 所围成的图形的面积.(结果保留π)
所围成的图形的面积.(结果保留π)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com