
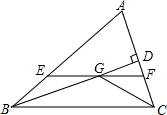
 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点G,过点G作EF∥BC交AB于E,交AC于F,过点G作GD⊥AC于D,下列四个结论:
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点G,过点G作EF∥BC交AB于E,交AC于F,过点G作GD⊥AC于D,下列四个结论:分析 ①根据∠ABC和∠ACB的平分线相交于点G可得出∠EBG=∠CBG,∠BCG=∠FCG,再由EF∥BC可知∠CBG=∠EGB,∠BCG=∠CGF,故可得出BE=EG,GF=CF,由此可得出结论;
②先根据角平分线的性质得出∠GBC+∠GCB=$\frac{1}{2}$(∠ABC+∠ACB),再由三角形内角和定理即可得出结论;
③根据三角形内心的性质即可得出结论;
④连接AG,根据三角形的面积公式即可得出结论.
解答 解:①∵∠ABC和∠ACB的平分线相交于点G,
∴∠EBG=∠CBG,∠BCG=∠FCG.
∵EF∥BC,
∴∠CBG=∠EGB,∠BCG=∠CGF,
∴∠EBG=∠EGB,∠FCG=∠CGF,
∴BE=EG,GF=CF,
∴EF=EG+GF=BE+CF,故本小题正确;
②∵∠ABC和∠ACB的平分线相交于点G,
∴∠GBC+∠GCB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$(180°-∠A),
∴∠BGC=180°-(∠GBC+∠GCB)=180°-$\frac{1}{2}$(180°-∠A)=90°+$\frac{1}{2}$ ∠A,故本小题正确;
∠A,故本小题正确;
③∵∠ABC和∠ACB的平分线相交于点G,
∴点G是△ABC的内心,
∴点G到△ABC各边的距离相等,故本小题正确;
④连接AG,
∵点G是△ABC的内心,GD=m,AE+AF=n,
∴S△AEF=$\frac{1}{2}$AE•GD+$\frac{1}{2}$AF•GD=$\frac{1}{2}$(AE+AF)•GD=$\frac{1}{2}$nm,故本小题错误.
故答案为:①②③.
点评 本题考查的是等腰三角形的判定与性质,熟知角平分线的性质、三角形内角和定理及三角形内心的性质是解答此题的关键.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:选择题
| A. | 4a2-4a+1=4a(a-1)+1 | B. | x2-4y2=(x+4y)(x-4y) | ||
| C. | $\frac{9}{4}$x2-x+$\frac{1}{9}$=($\frac{3}{2}$x-$\frac{1}{3}$)2 | D. | 2xy-x2-y2=-(x+y)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知:正方形ABCD和正方形AEFG,AD=2,AE=2$\sqrt{2}$,将正方形ABCD绕点A逆时针旋转,如图,当G恰好落在线段DB的延长线上时,则BE的长=$\sqrt{2}$+$\sqrt{6}$.
已知:正方形ABCD和正方形AEFG,AD=2,AE=2$\sqrt{2}$,将正方形ABCD绕点A逆时针旋转,如图,当G恰好落在线段DB的延长线上时,则BE的长=$\sqrt{2}$+$\sqrt{6}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 48cm2 | B. | 24cm2 | C. | 16cm2 | D. | 11cm2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com