|
|
|
下列说法正确的是
|
| [ ] |
A. |
四边相等的四边形是正方形
|
B. |
四角相等的四边形是正方形
|
C. |
对角线互相垂直的平行四边形是正方形
|
D. |
对角线互相垂直平分且相等的四边形是正方形
|
|
|
练习册系列答案
相关习题
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
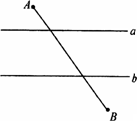
如图,已知直线a∥b,且a与b之间的距离为4,点A到直线a的距离为2,点B到直线b的距离为3, ,试在直线a上找一点M,在直线b上找一点N,满足MN⊥直线a,且AM+MN+NB的长度和最短,则此时AM+NB= ,试在直线a上找一点M,在直线b上找一点N,满足MN⊥直线a,且AM+MN+NB的长度和最短,则此时AM+NB=
|
| [ ] |
A. |
6
|
B. |
8
|
C. |
10
|
D. |
12
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
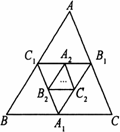
如图,A1、B1、C1分别是BC、AC、AB的中点,A2、B2、C2分别是B1C1、A1C1、A1B1的中点,这样延续下去.已知△ABC的周长是1,△A1B1C1的周长是L1,△A2B2C2的周长是L2,△AnBnCn的周长是Ln,则Ln=________.
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
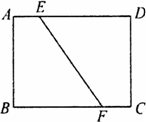
如图,有一矩形纸片ABCD,AB=6 cm,BC=8 cm,将纸片沿EF折叠,使点B与点D重合,再将纸片展开,求拆痕EF的长.
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
平行四边形ABCD的对角线AC、BD相交于点O,下列条件中,不能判定四边形ABCD是菱形的为
|
| [ ] |
A. |
AB=AD
|
B. |
AC⊥BD
|
C. |
∠A=∠D
|
D. |
CA平分∠BCD
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
四边形ABCD的对角线AC、BD相交于点O,有以下论断:①AB=BC;②∠DAB=90°;③BO=DO,AO=CO;④矩形ABCD;⑤菱形ABCD;⑥正方形ABCD.则下列推理中不正确的是
|
| [ ] |
A. |
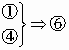
|
B. |
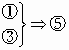
|
C. |
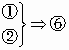
|
D. |
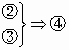
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
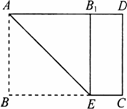
如图,矩形纸片ABCD中,AB=6 cm,BC=8 cm,现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CE的长为
|
| [ ] |
A. |
6 cm
|
B. |
4 cm
|
C. |
2 cm
|
D. |
1 cm
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
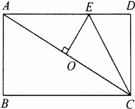
如图,在矩形ABCD中,AB=2,BC=4,对角线AC的垂直平分线分别交AD、AC于点E、O,连接CE,则CE的长为
|
| [ ] |
A. |
3
|
B. |
3.5
|
C. |
2.5
|
D. |
2.8
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
如图,在正方形ABCD中,E为CD边上一点,F为BC边延长线上一点,CE=CF.

(1)观察猜想BE和DF的大小关系,并证明你的猜想;
(2)若∠BEC=60°,求∠EFD的度数.
|
|
|
查看答案和解析>>

 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案