
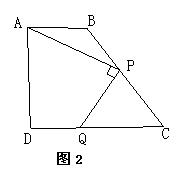
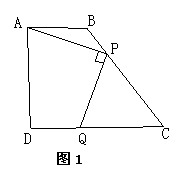
如图,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,
![]() ,
,![]() 是腰
是腰![]() 上一个动点(不含点
上一个动点(不含点![]() ),作
),作![]() 交
交![]() 于点
于点![]() (图
(图![]() )
)
(1)求![]() 的长与梯形
的长与梯形![]() 的面积;
的面积;
(2)当![]() 时,求
时,求![]() 的长;(图
的长;(图![]() )
)
解:(1)如图过B点作BE![]() CD,垂足为E
CD,垂足为E
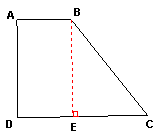 在Rt
在Rt![]() BEC中,
BEC中,![]() BEC=90度, tanC=
BEC=90度, tanC=![]() ,AD=BE=4
,AD=BE=4
∴ tanC=![]()
![]() ,CE=3
,CE=3
由勾股定理可得BC=5
![]() AB=DE=2
AB=DE=2 ![]()
∴CD=5
∴ S梯形ABCD=![]()
(2)
解法一:如图过点P作PN![]() CD,交CD于点N,交AB 的延长线于M
CD,交CD于点N,交AB 的延长线于M
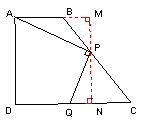
已知条件可知点P是点D沿AQ翻折而得到的,推得AP=4
![]() 梯形ABCD ∴AB∥CD ∴∠MBP=∠C
梯形ABCD ∴AB∥CD ∴∠MBP=∠C
在Rt![]() BMP中,∠BMP=90度,BP=x ,tan∠BMP=tan∠C=
BMP中,∠BMP=90度,BP=x ,tan∠BMP=tan∠C=![]()
![]()
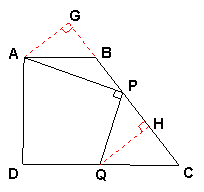 可推得MP=
可推得MP=![]() ,BM=
,BM=![]()
在Rt![]() AMP中,利用勾股定理可推得
AMP中,利用勾股定理可推得
![]() 即
即![]()
整理方程得![]()
解之满足条件的![]() 。
。
解法二:
解:过点Q作QH![]() BC,垂足为H,过点A
BC,垂足为H,过点A
作AG![]() BC,交BC的延长线于点G.
BC,交BC的延长线于点G.
由题意可知:AP=4
∵梯形ABCD ∴AB∥CD ∴∠ABG=∠C
∵AB=2,tan∠ABG=tan∠C=![]()
∴可通过解直角三角形得AG=![]() BG=
BG=![]()
在Rt![]() APG中,利用勾股定理可得
APG中,利用勾股定理可得![]() 即
即![]()
化简得![]() ,以下解法同上。
,以下解法同上。
解法三:
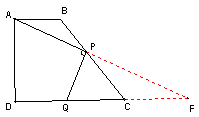 解:如图延长AP与DC相交于点F,可推得AP=4
解:如图延长AP与DC相交于点F,可推得AP=4
由已知可得AB=2,BP=x,CP=5-x
利用相似三角形的知识或平行线截线段成比例
定理可得![]()
在Rt![]() ADF中,∠D=90度,
ADF中,∠D=90度,![]()
即![]() 。
。
化简得![]() ,以下解法同解法一、二。
,以下解法同解法一、二。


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:
 如图,在梯形中ABCD中,AD∥BC,∠ABC=90°,BE⊥CD于点E,AB=BE.
如图,在梯形中ABCD中,AD∥BC,∠ABC=90°,BE⊥CD于点E,AB=BE.查看答案和解析>>
科目:初中数学 来源:2012届上海市松江初三二模数学试卷(带解析) 题型:解答题
如图,在梯形 中,
中, ∥
∥ ,
, ,
, ,点
,点 在对角线
在对角线 上,作
上,作 ,连接
,连接 ,且满足
,且满足 .
.
(1)求证: ;
;
(2)当 时,试判断四边形
时,试判断四边形 的形状,并说明理由.
的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源:初二年级第一学期期末考试练习四数学卷 题型:解答题
(本题6分) 如图,在梯形 中,
中, 两点在边
两点在边 上,且四边形
上,且四边形 是平行四边形.
是平行四边形.

1.(1) 与
与 有何等量关系?请说明理由;
有何等量关系?请说明理由;
2.(2)当 时,求证:平行四边形
时,求证:平行四边形 是矩形.
是矩形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com