
(2005 北京东城)如图所示,△ABO中,OA=OB,以O为圆心的圆经过AB中点C,且分别交OA、OB于点E、F.
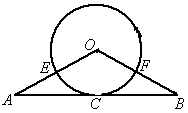
(1)求证AB是⊙O的切线;
(2)若△ABO腰上的高等于底边的一半,且 ,求
,求 的长.
的长.
|
解 (1)证明 如图
连接OC. ∵OA=OB,AC=BC, ∴OC⊥AB. 故AB是⊙O的切线. (2) 过B点作BD⊥AO,交AO延长线于D点,由题意有AB=2BD,由题目条件,有 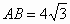 . .
在直角三角形 ABD中,根据正弦定义 . .
∴∠ A=30°.在直角三角形 ACO中,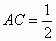 , ,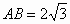 ,∠A=30°,则AO=2OC. ,∠A=30°,则AO=2OC.
由勾股定理,求得 OC=2.∵ OA=OB,且∠A=30°,∴∠AOB=120°.由弧长公式可求得 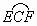 的长为 的长为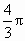 . . |
|
点评 本题是一道圆与三角形相结合的综合题目,涉及到圆的切线、直角三角形、勾股定理、三角函数的定义等多方面的知识,运用了数形结合的思想.考查范围广,是一道体现学生知识能力水平高低的好题. |


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:013
(2005 北京东城)如图所示,电线杆AB的中点C处有一标志物,在地面D点处测得标志物的仰角为45°,若点D到电线杆底部点B的距离为a,则电线杆AB的长可表示为
[ ]
|
A.a |
B.2a |
C. |
D. |
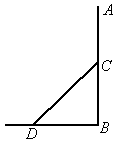
查看答案和解析>>
科目:初中数学 来源: 题型:044
(2005 北京东城)已知抛物线 .
.
(1)求证此抛物线与x轴有两个不同的交点;
(2)若m是整数,抛物线 与x轴交于整数点,求m的值;
与x轴交于整数点,求m的值;
(3)在(2)的条件下,设抛物线顶点为A,抛物线与x轴的两个交点中右侧交点为B.若M为坐标轴上一点,且MA=MB,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:022
(2005 北京东城)某校九年级(2)班想举办班徽设计比赛,全班50名同学,计划每位同学设计方案一份,拟评选出10份为一等奖,那么该班某位同学获一等奖的概率为________.
查看答案和解析>>
科目:初中数学 来源: 题型:013
(2005 北京东城)同时抛掷两枚质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数,下列事件中是不可能事件的是
[ ]
A.点数之和为12
B.点数之和小于3
C.点数之和大于4且小于8
D.点数之和为13
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com