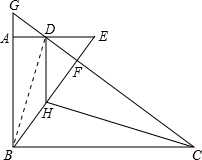
(1)解:连接BD,
由∠ABC=90°,AD∥BC得∠GAD=90°,
又∵BF⊥CD,
∴∠DFE=90°
又∵DG=DE,∠GDA=∠EDF,
∴△GAD≌△EFD,
∴DA=DF,
又∵BD=BD,
∴Rt△BAD≌Rt△BFD(HL),
∴BF=BA=

,∠ADB=∠BDF
又∵CF=6,
∴BC=
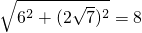
,
又∵AD∥BC,
∴∠ADB=∠CBD,
∴∠BDF=∠CBD,
∴CD=CB=8.
(2)证明:∵AD∥BC,
∴∠E=∠CBF,
∵∠HDF=∠E,
∴∠HDF=∠CBF,
由(1)得,∠ADB=∠CBD,
∴∠HDB=∠HBD,
∴HD=HB,
由(1)得CD=CB,
∴△CDH≌△CBH,
∴∠DCH=∠BCH,
∴∠BCH=

∠BCD=
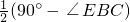
=
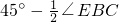
.
分析:(1)连接BD,由题意得出∠GAD=90°,从而证明△GAD≌△EFD,得出DA=DF再证明Rt△BAD≌Rt△BFD,利用勾股定理求出BC,继而得出线段CD的长.
(2)结合(1)可得出∠ADB=∠CBD,CD=CB,然后证明△CDH≌△CBH,得出∠DCH=∠BCH后,即可得出结论.
点评:此题考查了梯形、全等三角形的判定及性质,综合性较强,解答本题的关键是利用三角形全等的知识,将已知线段进行转化,另外要注意等角代换的应用,难度较大.

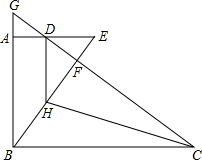 ,延长CD交BA的延长线于G,且DG=DE,AB=
,延长CD交BA的延长线于G,且DG=DE,AB= ,CF=6.
,CF=6. ∠EBC.
∠EBC. (1)解:连接BD,
(1)解:连接BD, ,∠ADB=∠BDF
,∠ADB=∠BDF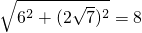 ,
, ∠BCD=
∠BCD=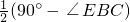 =
=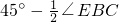 .
.

 如图,梯形ABCD中,已知AD∥BC,∠A=90°,AB=7,AD=2,cosC=
如图,梯形ABCD中,已知AD∥BC,∠A=90°,AB=7,AD=2,cosC=