
【题目】甲、乙两条轮船同时从港口A出发,甲轮船以每小时30海里的速度沿着北偏东60°的方向航行,乙轮船以每小时15海里的速度沿着正东方向行进,1小时后,甲船接到命令要与乙船会合,于是甲船改变了行进的速度,沿着东南方向航行,结果在小岛C处与乙船相遇.假设乙船的速度和航向保持不变,求:
(1)港口A与小岛C之间的距离;
(2)甲轮船后来的速度.

 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】近年来网约车十分流行,初三某班学生对“美团”和“滴滴”两家网约车公司各10名司机月收入进行了一项抽样调查,司机月收入(单位:千元)如图所示:


根据以上信息,整理分析数据如下:
平均月收入/千元 | 中位数/千元 | 众数/千元 | 方差/千元2 | |
“美团” | ① | 6 | 6 | 1.2 |
“滴滴” | 6 | ② | 4 | ③ |
(1)完成表格填空;
(2)若从两家公司中选择一家做网约车司机,你会选哪家公司,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB和抛物线的交点是A(0,-3),B(5,9),已知抛物线的顶点D的横坐标是2.

(1)求抛物线的解析式及顶点坐标;
(2)在![]() 轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(4,3)是反比例函数y=![]() 在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=
在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=![]() 的图象于点P.
的图象于点P.
(1)求反比例函数y=![]() 的表达式;
的表达式;
(2)求点B的坐标;
(3)求△OAP的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
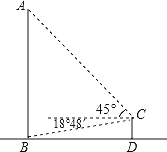
【题目】全球最大的关公塑像矗立在荆州古城东门外.如图,张三同学在东门城墙上C处测得塑像底部B处的俯角为18°48′,测得塑像顶部A处的仰角为45°,点D在观测点C正下方城墙底的地面上,若CD=10米,则此塑像的高AB约为 米(参考数据:tan78°12′≈4.8).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,∠A=30°,BC=6,D,E分别是AB,AC边的中点,将△ABC绕点B顺时针旋转60°到△A′BC′的位置,则整个旋转过程中线段DE所扫过部分的面积(即图中阴影部分面积)为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点 O 是△ABC 的边 AB 上一点,以 OB 为半径的⊙O 交 BC 于点 D,过点 D 的切线交 AC 于点 E,且 DE⊥AC.
(1)证明:AB=AC;
(2)设 AB=![]() cm,BC=2cm,当点 O 在 AB 上移动到使⊙O 与边 AC 所在直线相切时, 求⊙O 的半径.
cm,BC=2cm,当点 O 在 AB 上移动到使⊙O 与边 AC 所在直线相切时, 求⊙O 的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,则下列结论中:①ac>0;②a+b+c<0;③4a﹣2b+c<0;④2a+b<0;⑤4ac﹣b2<4a;⑥a+b>0中,其中正确的个数为( )
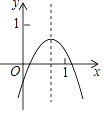
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
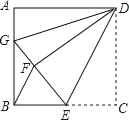
【题目】如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG、BF,给出下列结论:①△DAG≌△DFG;②BG=2AG;③△EBF∽△DEG;④S△BEF=![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com