
如图,在矩形ABCD中,AD>AB,将矩形ABCD折叠,使点C与点A重合,折痕为MN,连结CN.若△CDN的面积与△CMN的面积比为1︰5,则 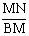 的值为( ).
的值为( ).
A.2 B.4 C. D.
D.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
某种树木的分枝生长规律如图所示,则预计到第6年时,树木的分枝数为 .
| 年 份 | 分 枝 数 |
| 第1年 | 1 |
| 第2年 | 1 |
| 第3年 | 2 |
| 第4年 | 3 |
| 第5年 | 5 |
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
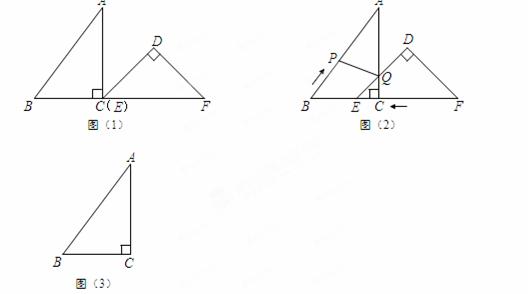
已知:把Rt△ABC和Rt△DEF按如图(1)摆放(点C与点E重合),点B、C(E)、F在同一条直线上.∠ACB = ∠EDF = 90°,∠DEF = 45°,AC = 8 cm,BC = 6 cm,EF = 9 cm。
如图(2),△DEF从图(1)的位置出发,以1 cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点B出发,以2 cm/s的速度沿BA向点A匀速移动。当△DEF的顶点D移动到AC边上时,△DEF停止移动,点P也随之停止移。DE与AC相交于点Q,连接PQ,设移动时间为t(s)(0<t<4.5)。解答下列问题:
(1)当t为何值时,点A在线段PQ的垂直平分线上?
(2)连接PE,设四边形APEC的面积为y(cm2),求y与t之间的函数关系式;是否存在某一时刻t,使面积y最小?若存在,求出y的最小值;若不存在,说明理由。
(3)是否存在某一时刻t,使P、Q、F三点在同一条直线上?若存在,求出此时t的值;若不存在,说明理由。(图(3)供同学们做题使用)
查看答案和解析>>
科目:初中数学 来源: 题型:
某人骑车沿直线旅行,先前进了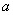 千米,休息了一段时间,又原路原速返回了
千米,休息了一段时间,又原路原速返回了 千米(
千米(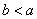 ),再掉头沿原方向以比原速大的速度行驶,则此人离起点的距离
),再掉头沿原方向以比原速大的速度行驶,则此人离起点的距离 与时间
与时间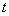 的函数关系的大致图象是( ).
的函数关系的大致图象是( ). 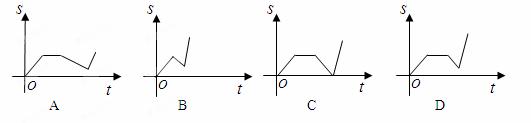
查看答案和解析>>
科目:初中数学 来源: 题型:
将长度为12厘米的线段截成两条线段a、b(a、b长度均为整数).如果截成的a、b长度分别相同算作同一种截法(如:a=9,b=1和a=1,b=9为同一种截法),那么以截成的a、b为对角线,以另一条c=4厘米长的线段为一边,能构成平行四边形的概率是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
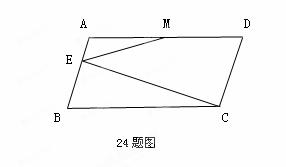
如图,在□ABCD中,点M为边AD的中点,过点C作AB的垂线交AB于点E,连接ME.
(1)若AM=2AE=4,∠BCE=30°,求□ABCD的面积;
(2)若BC=2AB,求证:∠EMD=3∠MEA.
查看答案和解析>>
科目:初中数学 来源: 题型:
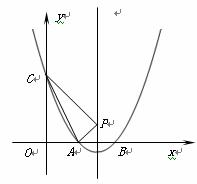
如图1,抛物线 与
与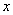 轴交于
轴交于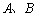 两点,与
两点,与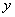 轴交于点
轴交于点 ,连结AC,若
,连结AC,若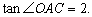
(1)求抛物线的解析式;
(2)抛物线对称 轴上有一动点P,当
轴上有一动点P,当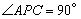 时,求出点
时,求出点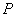 的坐标;
的坐标;
(3)如图2所示,连结 ,
, 是线段
是线段 上(不与
上(不与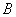 、
、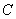 重合)的一个动点.过点
重合)的一个动点.过点 作直线
作直线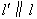 ,交抛物线于点
,交抛物线于点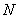 ,连结
,连结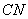 、
、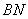 ,设点
,设点 的横坐标为.当t为何值时,
的横坐标为.当t为何值时,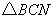 的面积最大?最大面积为多少?
的面积最大?最大面积为多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com