
【题目】如图,点O是Rt△ABC的AB边上一点,∠ACB=90°,⊙O与AC相切于点D,与边AB,BC分别相交于点E,F.
(1)求证:DE=DF;
(2)当BC=3,sinA=![]() 时,求AE的长.
时,求AE的长.
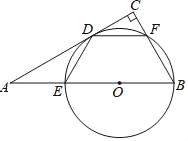
【答案】(1)见解析;(2)AE=![]() .
.
【解析】
(1)连接OD,OF,由切线的性质可得∠ADO=90°,从而得到OD∥BC,从而得到∠AOD=∠ABC,∠DOF=∠OFB,并由半径相等,再进行角的代换从而得到∠AOD=∠DOF,即可求解.
(2) Rt△ABC中,有正弦的定义求出AB,再由Rt△AOD中,设圆的半径为r,通过正弦建立比例式方程从而进行求解.
解:(1)如图所示,连接OD,OF,
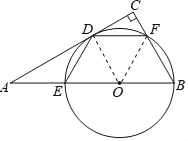
∵⊙O与AC相切于点D,
∴∠ADO=90°,
∵∠ACB=90°,
∴OD∥BC,
∴∠AOD=∠ABC,∠DOF=∠OFB,
∵OB=OF,
∴∠ABC=∠OFB,
∴∠AOD=∠DOF,
∴DE=DF;
(2)在Rt△ABC中,∵BC=3,sinA=![]() =
=![]() ,
,
∴AB=5,
设⊙O的半径为r,则OB=OD=OE=r,
则AO=AB﹣OB=5﹣r,AE=5﹣2r,
在Rt△AOD中,∵sinA=![]() =
=![]() ,
,
∴![]() =
=![]() ,解得r=
,解得r=![]() ,
,
则AE=5﹣2r=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
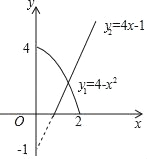
【题目】有一种市场均衡模型是用一次函数和二次函数来刻化的:根据市场调查,某种商品的市场需求量y1(吨)与单价x(百元)之间的关系可看作是二次函数y1=4﹣x2,该商品的市场供应量y2(吨)与单价x(百元)之间的关系可看作是一次函数y2=4x﹣1.
(1)当需求量等于供应量时,市场达到均衡.此时的单价x(百元)称为均衡价格,需求量(供应量)称为均衡数量.求所述市场均衡模型的均衡价格和均衡数量.
(2)当该商品单价为50元时,此时市场供应量与需求量相差多少吨?
(3)根据以上信息分析,当该商品①供不应求②供大于求时,该商品单价分别会在什么范围内?
查看答案和解析>>
科目:初中数学 来源: 题型:
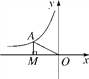
【题目】如图,反比例函数y=![]() 的图象在第二象限内,点A是图象上的任意一点,AM⊥x轴于点M,O是原点.若S△AOM=3,求该反比例函数的解析式,并写出自变量的取值范围.
的图象在第二象限内,点A是图象上的任意一点,AM⊥x轴于点M,O是原点.若S△AOM=3,求该反比例函数的解析式,并写出自变量的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张矩形纸板按图中虚线裁剪成九块,其中有两块是边长都为![]() 的大正方形,两块是边长都为
的大正方形,两块是边长都为![]() 的小正方形,五块是长为
的小正方形,五块是长为![]() 、宽为
、宽为![]() 的全等小矩形,且
的全等小矩形,且![]() >
> ![]() .(以上长度单位:cm)
.(以上长度单位:cm)
(1)观察图形,可以发现代数式![]() 可以因式分解为 ;
可以因式分解为 ;
(2)若每块小矩形的面积为10![]() ,四个正方形的面积和为58
,四个正方形的面积和为58![]() ,试求图中所有裁剪线(虚线部分)长之和.
,试求图中所有裁剪线(虚线部分)长之和.

查看答案和解析>>
科目:初中数学 来源: 题型:
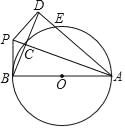
【题目】如图,AB是⊙O的直径,点D是⊙O外一点,AB=AD,BD交⊙O于点C,AD交⊙O于点E,点P是AC的延长线上一点,连接PB、PD,且PD⊥AD
(1)判断PB与⊙O的位置关系,并说明理由;
(2)连接CE,若CE=3,AE=7,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AD⊥BC,垂足为D.给出下列四个结论:①sinα=sinB;②sinβ=sinC;③sinB=cosC;④sinα=cosβ.其中正确的结论有_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数学实践活动小组要测量学校附近楼房CD的高度,在水平底面A处安置侧倾器测得楼房CD顶部点D的仰角为30°,向前走20米到达E处,测得点D的仰角为60°.已知侧倾器AB的高度为1.6米,则楼房CD的高度约为(结果精确到0.1米)( )
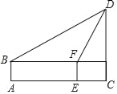
A. 30米 B. 18.9米 C. 32.6米 D. 30.6米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011山东济南,22,3分)如图1,△ABC中,∠C=90°,∠ABC=30°,AC=m,延长CB至点D,使BD=AB.
①求∠D的度数;
②求tan75°的值.
(2)如图2,点M的坐标为(2,0),直线MN与y轴的正半轴交于点N,∠OMN=75°.求直线MN的函数表达式.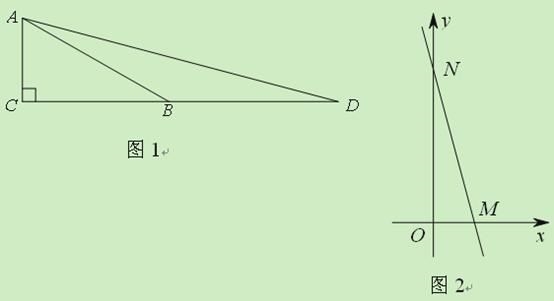
查看答案和解析>>
科目:初中数学 来源: 题型:
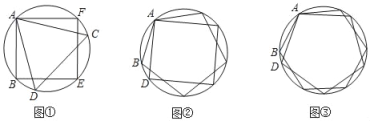
【题目】如图①,正三角形和正方形内接于同一个圆;如图②,正方形和正五边形内接于同一个圆;如图③,正五边形和正六边形内接于同一个圆;…;则对于图①来说,BD可以看作是正_____边形的边长;若正n边形和正(n+1)边形内接于同一个圆,连接与公共顶点相邻同侧两个不同正多边形的顶点可以看做是_____边形的边长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com