
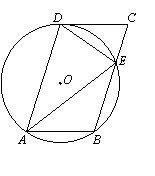
25.如图,在□ABCD中,过A、B、D三点的⊙O交BC于点E,连接DE,∠CDE=∠DAE.
(1)判断四边形ABED的形状,并说明理由;
(2)判断直线DC与⊙O的位置关系,并说明理由;
(3)若AB=3,AE=6,求CE的长.
 |
(1)四边形ABED是等腰梯形.
理由如下:在□ABCD中,AD∥BC,
∴∠DAE=∠AEB.
 ∴
∴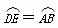 ,DE=AB.
,DE=AB.
∵AB∥CD,∴AB与DE不平行.
∴四边形ABDE是等腰梯形.
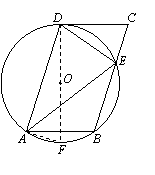
(2)直线DC与⊙O相切.
如图,作直径DF,连接AF.
于是,∠EAF=∠EDF.
 ∵∠DAE=∠CDE,
∵∠DAE=∠CDE,
∴∠EAF+∠DAE=∠EDF+∠CDE,即∠DAF=∠CDF.
∵DF是⊙O的直径,点A在⊙O上,
∴∠DAF=90°,∴∠CDF=90°.∴OD⊥CD.
直线DC经过⊙O半径OD外端D,且与半径垂直,
直线DC与⊙O相切.
(3)由(1),∠EDA=∠DAB.
在□ABCD中,∠DAB=∠DCB,
∴∠EDA=∠DCB.又∵∠DAE=∠CDE,∴△ADE∽△DCE.∴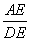 =
=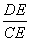 ,
,
∵AB=3,由(1)得,AB=DE=DC=3.即 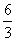 =
=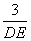 .
.
解得,CE=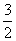 .
.


 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
为响应推进中小学生素质教育的号召,某校决定在下午15点至16点开设以下选修课:音乐史、管乐、篮球、健美操、油画.为了解同学们的选课情况,某班数学兴趣小组从全校三个年级中 各调查一个班级,根据相关数据,绘制如下统计图.
各调查一个班级,根据相关数据,绘制如下统计图.
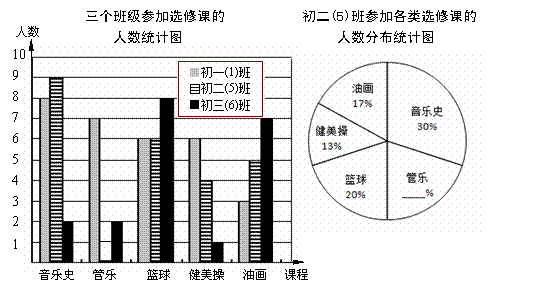 |
(1)请根据以上信息,直接补全条形统计图和扇形统计图;
(2)若初一年级有180人,请估算初一年级中有多少学生选修音乐史?
(3)若该校共有学生540人,请估算全校有多少学生选修篮球课?
查看答案和解析>>
科目:初中数学 来源: 题型:
如果两个多边形不仅相似(相似比不等于1),而且有一条公共边,那么就称这两个多边形是共边相似多边形.例如,图①中,△ABC与△ACD是共AC边相似三角形,图②中,□ABCD与□CEFD是共CD边相似四边形.
 |
(1)判断下列命题的真假(在相应括号内填上“真”或“假”):
①正三角形的共边相似三角形是正三角形.( )
②如果两个三角形是位似三角形,那么这两个三角形不可能是共边相似三角形.( )
(2)如图③,在△ABC中,∠C=90°,∠A=50°,画2个不全等的三角形,使这2个三角形均是与△ABC共BC边的相似三角形.(要求:画图工具不限,不写画法,保留画图痕迹或有必要的说明)
(3)图④是相邻两边长分别为a、b(a>b)的矩形,图⑤是边长为c的菱形,图⑥是两底长分别为d、e,腰长为f(0<e-d<2f)的等腰梯形,判断这三个图形是否存在共边相似四边形?如果存在,直接写出它们的共边相似四边形各边的长度.
 |
(4)根据(1)、(2)和(3)中获得的经验回答:如果一个多边形存在它的共边相似多边形,那么它必须满足条件: .
查看答案和解析>>
科目:初中数学 来源: 题型:
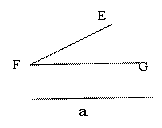
如图,已知线段a及∠EFG.
(1)只用直尺和圆规,求作⊿ABC,使BC=a, ∠B=∠EFG, ∠C=2∠B(在指定作图区域作图,保留作图痕迹,不写作法);
 (2)在⊿ABC中作BC的中垂线分别交AB、BC于点M、N,如果SinB=
(2)在⊿ABC中作BC的中垂线分别交AB、BC于点M、N,如果SinB= ,求⊿BMN与⊿ABC的面积之比。
,求⊿BMN与⊿ABC的面积之比。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com