
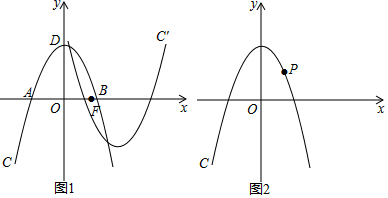
���� ��1�������������ߵĶ���C��0��4����A��-2$\sqrt{2}$��0�����������ߵĽ���ʽΪy=ax2+4����A��2$\sqrt{2}$��0������ɵ�a=-$\frac{1}{2}$���ɴ˼��ɽ�����⣻
��2��������������C��Ķ�������Ϊ��2m��-4������������C��Ľ���ʽΪy=$\frac{1}{2}$��x-2m��2-4����$\left\{\begin{array}{l}{y=-\frac{1}{2}{x}^{2}+4}\\{y=\frac{1}{2}��x-2m��^{2}-4}\end{array}\right.$����ȥy�õ�x2-2mx+2m2-8=0�������⣬������C����������C��y����Ҳ���������ͬ�Ĺ����㣬����$\left\{\begin{array}{l}{��2m��^{2}-4��2{m}^{2}-8����0}\\{2m��0}\\{2{m}^{2}-8��0}\end{array}\right.$���ⲻ��ʽ�鼴�ɽ�����⣻
��3������1���ı���PMP��N�ܳ�Ϊ�����Σ���PE��x����E��MH��x����H����������֪P��2��2��������PFM�ǵ���ֱ��������ʱ���ı���PMP��N�������Σ��Ƴ�PF=FM����PFM=90�㣬��֤��PFE�ա�FMH���ɵ�PE=FH=2��EF=HM=2-m���ɵ�M��m+2��m-2�������ɴ���ϵ�������ɽ�����⣻����2����ͼ���ı���PMP��N�������Σ�ͬ���ɵ�M��m-2��2-m�������ô���ϵ�������ɽ�����⣮
��� �⣺��1�������������ߵĶ���C��0��4����A��-2$\sqrt{2}$��0�����������ߵĽ���ʽΪy=ax2+4��
��A��-2$\sqrt{2}$��0������ɵ�a=-$\frac{1}{2}$��
��������C�ĺ�������ʽΪy=-$\frac{1}{2}$x2+4��
��2��������������C��Ķ�������Ϊ��2m��-4������������C��Ľ���ʽΪy=$\frac{1}{2}$��x-2m��2-4��
��$\left\{\begin{array}{l}{y=-\frac{1}{2}{x}^{2}+4}\\{y=\frac{1}{2}��x-2m��^{2}-4}\end{array}\right.$����ȥy�õ�x2-2mx+2m2-8=0��
�����⣬������C����������C��y����Ҳ���������ͬ�Ĺ����㣬
����$\left\{\begin{array}{l}{��2m��^{2}-4��2{m}^{2}-8����0}\\{2m��0}\\{2{m}^{2}-8��0}\end{array}\right.$�����2��m��2$\sqrt{2}$��
������������m��ȡֵ��ΧΪ2��m��2$\sqrt{2}$��
��3�����ۣ��ı���PMP��N�ܳ�Ϊ�����Σ�
���ɣ�1����1����ͼ����PE��x����E��MH��x����H��
��������֪P��2��2��������PFM�ǵ���ֱ��������ʱ���ı���PMP��N�������Σ�
��PF=FM����PFM=90�㣬
��֤��PFE�ա�FMH���ɵ�PE=FH=2��EF=HM=2-m��
��M��m+2��m-2����
�ߵ�M��y=-$\frac{1}{2}$x2+4�ϣ�
��m-2=-$\frac{1}{2}$��m+2��2+4�����m=$\sqrt{17}$-3��-$\sqrt{17}$-3����������
��m=$\sqrt{17}$-3ʱ���ı���PMP��N�������Σ�
����2����ͼ���ı���PMP��N�������Σ�ͬ���ɵ�M��m-2��2-m����
��M��m-2��2-m������y=-$\frac{1}{2}$x2+4��2-m=-$\frac{1}{2}$��m-2��2+4�����m=6��0����������
��m=6ʱ���ı���PMP��N�������Σ�
���ϣ��ı���PMP��N�ܳ�Ϊ�����Σ�m=$\sqrt{17}$-3��6��
���� ���⿼����κ����ۺ��⡢���ĶԳƱ任�������ε����ʡ�ȫ�������ε��ж������ʡ�һԪ���η��̵ĸ���ϵ���Ĺ�ϵ��֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ�����ò����������̽�����⣬�����п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
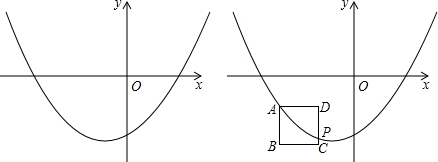
 ���壺�������ڽ�����ı��ν����Ƚ��ı��Σ�
���壺�������ڽ�����ı��ν����Ƚ��ı��Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
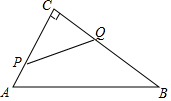 ��ͼ���ڡ�ABC�У���C=90�㣬AB=10cm��BC=8cm����P�ӵ�A��AC���C��1cm/s���ٶ��˶���ͬʱ��Q�ӵ�C��CB���B��2cm/s���ٶ��˶�����Q�˶�����Bֹͣ�������˶������У��ı���PABQ�������СֵΪ��������
��ͼ���ڡ�ABC�У���C=90�㣬AB=10cm��BC=8cm����P�ӵ�A��AC���C��1cm/s���ٶ��˶���ͬʱ��Q�ӵ�C��CB���B��2cm/s���ٶ��˶�����Q�˶�����Bֹͣ�������˶������У��ı���PABQ�������СֵΪ��������| A�� | 19cm2 | B�� | 16cm2 | C�� | 15cm2 | D�� | 12cm2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
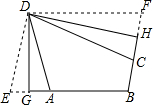
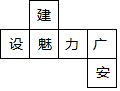 ��ͼ��һ��������ı���չ��ͼ����ԭ���������롰�ȡ������ڵ�����Ե����ϱ�����ǣ�������
��ͼ��һ��������ı���չ��ͼ����ԭ���������롰�ȡ������ڵ�����Ե����ϱ�����ǣ�������| A�� | �� | B�� | �� | C�� | �� | D�� | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
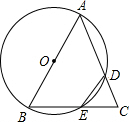 ��ͼ����֪�ȱߡ�ABC�ı߳�Ϊ6����ABΪֱ���ġ�O���AC��BC�ֱ���D��E���㣬���ӻ�$\widehat{DE}$�ij�Ϊ�У�
��ͼ����֪�ȱߡ�ABC�ı߳�Ϊ6����ABΪֱ���ġ�O���AC��BC�ֱ���D��E���㣬���ӻ�$\widehat{DE}$�ij�Ϊ�У��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
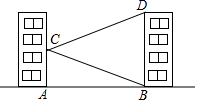 ��ͼ��ѧУ��ʵ��¥������һ����ѧ¥��С����ʵ��¥�Ĵ���C��ý�ѧ¥����D������Ϊ18�㣬��ѧ¥�ײ�B�ĸ���Ϊ20�㣬����ʵ��¥���ѧ¥֮��ľ���AB=30m��
��ͼ��ѧУ��ʵ��¥������һ����ѧ¥��С����ʵ��¥�Ĵ���C��ý�ѧ¥����D������Ϊ18�㣬��ѧ¥�ײ�B�ĸ���Ϊ20�㣬����ʵ��¥���ѧ¥֮��ľ���AB=30m���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com