
| 3,4,5 | 32+42=52 |
| 5,12,13, | 52+122=132 |
| 7,24,25 | 72+242=252 |
| 9,40,41 | 92+402=412 |
| … | … |
| 17,b,c | 172+b2=c2 |
分析 (1)根据表格找出规律再证明其成立;
(2)把已知数据代入经过证明成立的规律即可.
解答 解:(1)以上各组数的共同点可以从以下方面分析:
①以上各组数均满足a2+b2=c2;
②最小的数(a)是奇数,其余的两个数是连续的正整数;
③最小奇数的平方等于另两个连续整数的和,
如32=9=4+5,52=25=12+13,72=49=24+25,92=81=40+41…
由以上特点我们可猜想并证明这样一个结论:
设m为大于1的奇数,将m2拆分为两个连续的整数之和,即m2=n+(n+1),
则m,n,n+1就构成一组简单的勾股数,
证明:∵m2=n+(n+1)(m为大于1的奇数),
∴m2+n2=2n+1+n2=(n+1)2,
∴m,n,(n+1)是一组勾股数;
(2)运用以上结论,当a=17时,
∵172=289=144+145,
∴b=144,c=145.
点评 本题考查了勾股数、勾股定理的逆定理;解答此题要用到勾股定理的逆定理:已知三角形ABC的三边满足a2+b2=c2,则三角形ABC是直角三角形.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{4+9}=\sqrt{4}+\sqrt{9}$ | B. | 2$\sqrt{2}-\sqrt{2}$=2 | C. | $\sqrt{2}×\sqrt{3}=\sqrt{5}$ | D. | $\frac{{\sqrt{21}}}{{\sqrt{3}}}=\sqrt{\frac{21}{3}}=\sqrt{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
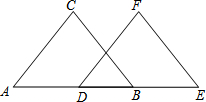 看图填空:已知,如图,BC∥EF,AD=BE,BC=EF.试说明△ABC≌△DEF
看图填空:已知,如图,BC∥EF,AD=BE,BC=EF.试说明△ABC≌△DEF查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知AE=CF,∠AFD=∠CEB,添加一个条件后,仍无法判定△ADF≌△CBE的是( )
如图,已知AE=CF,∠AFD=∠CEB,添加一个条件后,仍无法判定△ADF≌△CBE的是( )| A. | ∠A=∠C | B. | AD=CB | C. | BE=DF | D. | AD∥BC |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 点P的坐标为(1,2) | |
| B. | 关于x、y的方程组$\left\{\begin{array}{l}{y=x+1}\\{y=mx+n}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | |
| C. | 直线l1中,y随x的增大而减小 | |
| D. | 直线y=nx+m也经过点P |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com