
����Ŀ����ƽ��ֱ������ϵ�У�A(6��a)��B(b��0)��M(0��c)��P��Ϊy����һ���㣬��(b��2)2+|a��6|+![]() ��0��
��0��
(1)���B��M�����ꣻ
(2)��P�����߶�OM���˶�ʱ�������Ƿ����һ����PʹS��PAB��13�������ڣ������P���������AB�ij��ȣ��������ڣ���˵�����ɣ�
(3)����P���˶���ֱ��OM�ϵ��κ�λ��(��������O��M)����PAM����APB����PBO����֮���Ƿ���ij�̶ֹ���������ϵ������У���������ѧ֪ʶ�ҳ���֤�������û�У���˵�����ɣ�
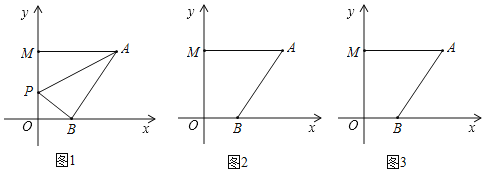
���𰸡���1��M��0��6����B��2��0����A��6��6������2��AB=2![]() ����3���ٵ���P���߶�OM��ʱ�����ۣ���APB+��PBO=��PAM�����ɼ��������ڵ���P��MO���ӳ�����ʱ�����ۣ���APB+��PBO=��PAM�����ɼ��������۵���P��OM���ӳ�����ʱ�����ۣ���PBO=��PAM+��APB�����ɼ�������
����3���ٵ���P���߶�OM��ʱ�����ۣ���APB+��PBO=��PAM�����ɼ��������ڵ���P��MO���ӳ�����ʱ�����ۣ���APB+��PBO=��PAM�����ɼ��������۵���P��OM���ӳ�����ʱ�����ۣ���PBO=��PAM+��APB�����ɼ�������
��������
��1�����÷Ǹ��������ʣ����a��b��c���ɽ�����⣻
��2����P��0��m��������S��PAB=S����AMOB-S��APM-S��PBO���������̼��ɽ�����⣻
��3�����������Σ��ֱ�ͼ�ν�����⼴����
��1���ߣ�b-2��2+|a-6|+![]() =0��
=0��
���ߣ�b-2��2����0��|a-6|��0��![]() ��0��
��0��
��a=6��b=2��c=6��
��M��0��6����B��2��0����A��6��6����
��2����P��0��m����
��S��PAB=13���ı���AMOB��ֱ�����Σ�
��![]() ��6+2��6-
��6+2��6-![]() m2-
m2-![]() ��6-m��6=13��
��6-m��6=13��
��m=![]() ��
��
��P��0��![]() ����
����
AB=![]() =2
=2![]() ��
��
��3������ͼ2-1�У�����P���߶�OM��ʱ�����ۣ���APB+��PBO=��PAM��
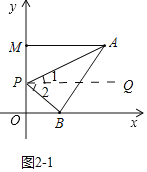
���ɣ���PQ��AM����PQ��AM��ON��
���1=��PAM����2=��PBO��
���1+��2=��PAM+��PBO��
����APB=��PAM+��PBO��
��APB+��PBO=��PAM��
����ͼ2-2����ʾ������P��MO���ӳ�����ʱ�����ۣ���APB+��PBO=��PAM��
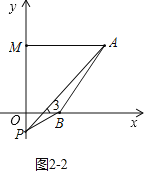
���ɣ���AM��OB��
���PAM=��3��
�ߡ�3=��APB+��PBO��
���APB+��PBO=��PAM��
����ͼ2-3�У�����P��OM���ӳ�����ʱ�����ۣ���PBO=��PAM+��APB��
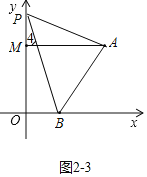
���ɣ���AM��OB��
���4=��PBO��
�ߡ�4=��PAM+��APB��
���PBO=��PAM+��APB��


 Сѧ�̲�ȫ��ϵ�д�
Сѧ�̲�ȫ��ϵ�д� Сѧ��ѧ������ѿڶ���ϵ�д�
Сѧ��ѧ������ѿڶ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У���E��N��P��G�ֱ��ڱ�AB��BC��CD��DA�ϣ���M��F��Q���ڶԽ���BD�ϣ����ı���MNPQ��AEFG��Ϊ�����Σ��� ![]() ��ֵ���� ��
��ֵ���� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD��������CEFG�߳��ֱ�Ϊa��b��������CEFG�Ƶ�C��ת���������н��ۣ���BE=DG����BE��DG����DE2+BG2=2a2+2b2��������ȷ�����У� ��

A. 0�� B. 1�� C. 2�� D. 3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������н���ƽ��ֱ������ϵ![]() ��ʹ��
��ʹ��![]() ��
��![]() ���������ֱ�Ϊ
���������ֱ�Ϊ![]() ��
��![]() ������
������![]() ��
��![]() ���ڵ�C��
���ڵ�C��
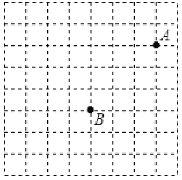
��1������Ҫ��ƽ��ֱ������ϵ![]() ���߶�
���߶�![]() ��д����
�����![]() ������__________��
������__________��
��2��ֱ��д����![]() ��
��![]() ��
��![]() �������������___________��
�������������___________��
��3�����߶�![]() �����߶�
�����߶�![]() ƽ�Ƶõ��ģ���
ƽ�Ƶõ��ģ���![]() �Ķ�Ӧ����
�Ķ�Ӧ����![]() ��д��һ�����߶�
��д��һ�����߶�![]() �õ��߶�
�õ��߶�![]() �Ĺ���________��
����________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y1=�� ![]() x+2��x�ᣬy��ֱ���B��C��������y=ax2+bx+c��a��0��������A��B��C����A����Ϊ����1��0����
x+2��x�ᣬy��ֱ���B��C��������y=ax2+bx+c��a��0��������A��B��C����A����Ϊ����1��0����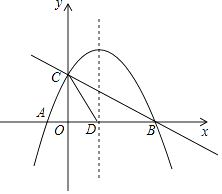
��1���������ߵĽ���ʽ��
��2�������ߵĶԳ�����x�ύ�ڵ�D������CD����P��ֱ��BC�Ϸ��������ϵ�һ���㣨����B��C�غϣ�������P�˶����δ�ʱ���ı���PCDB�������������ʱ�ı���PCDB��������ֵ�͵�P���ꣻ
��3�����������ϵĶԳ����ϣ��Ƿ����һ��M��ʹ|MA��MC|��ֵ����Ƿ����һ��N��ʹ��NCD����CDΪ���ĵ��������Σ������ڣ�ֱ��д����M����N�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڳ�����![]() �ڣ������ű߳��ֱ�Ϊ
�ڣ������ű߳��ֱ�Ϊ![]() ��
��![]() ��
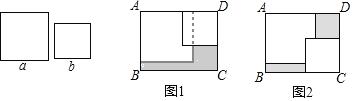
��![]() ����������ֽƬ��ͼ1��ͼ2���ַ�ʽ���ã�ͼ1��ͼ2������������ֽƬ���в����ص�������������δ��������������ֽƬ���ǵIJ�������Ӱ��ʾ����ͼ1����Ӱ���ֵ����Ϊ
����������ֽƬ��ͼ1��ͼ2���ַ�ʽ���ã�ͼ1��ͼ2������������ֽƬ���в����ص�������������δ��������������ֽƬ���ǵIJ�������Ӱ��ʾ����ͼ1����Ӱ���ֵ����Ϊ![]() ��ͼ2����Ӱ���ֵ������Ϊ
��ͼ2����Ӱ���ֵ������Ϊ![]() �������
�������![]() ��
��![]() �Ĵ�С��ϵ������ȷ���ǣ� ��
�Ĵ�С��ϵ������ȷ���ǣ� ��
A.![]() B.
B.![]() C.
C.![]() D.��ȷ��
D.��ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��ӵ�P1����1��0����P2����1����1����P3��1����1����P4��1��1����P5����2��1����P6����2����2������������չ��ȥ����P2017������Ϊ��������
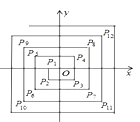
A. ��504��504�� B. ����504��504�� C. ����504����504�� D. ����505��504��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����OCDE����������ֱ���C��3��0����D��3��4����E��0��4������A��DE�ϣ���AΪ����������߹���C���ҶԳ���x=1��x���ڵ�B������EC��AC����P��QΪ���㣬���˶�ʱ��Ϊt�룮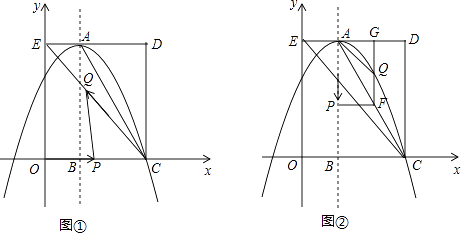
��1����գ���A����Ϊ�������ߵĽ���ʽΪ ��
��2����ͼ���У�����P���߶�OC�ϴӵ�O���C��1����λ/����ٶ��˶���ͬʱ����Q���߶�CE�ϴӵ�C���E��2����λ/����ٶ��˶�����һ���㵽���յ�ʱ����һ������ֹ֮ͣ�˶�����tΪ��ֵʱ����PCQΪֱ�������Σ�
��3����ͼ���У�����P�ڶԳ����ϴӵ�A��ʼ���B��1����λ/����ٶ��˶�������P��PF��AB����AC�ڵ�F������F��FG��AD�ڵ�G�����������ڵ�Q������AQ��CQ����tΪ��ֵʱ����ACQ�����������ֵ�Ƕ��٣�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com