【题目】某电脑公司经销甲种型号电脑，每台售价4000元．为了增加收入，电脑公司决定再经销乙种型号电脑．已知甲种电脑每台进价为3500元，乙种电脑每台进价为3000元，公司预计用不多于5万元且不少于4.8万元的资金购进这两种电脑共15台.
（1）有几种进货方案？
（2）如果乙种电脑每台售价为3800元，为打开乙种电脑的销路，公司决定每售出一台乙种电脑，返还顾客现金a元，要使（2）中所有方案获利相同，a值应是多少？ 若考虑投入成本最低，则应选择哪种进货方案？
名校课堂系列答案科目：初中数学 来源： 题型：
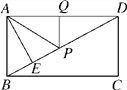
【题目】如图，在矩形ABCD中，AD＝6，AE⊥BD，垂足为E，DE＝3BE，点P，Q分别在BD，AD 上，则AP＋PQ的最小值为：
A. 2
B. C. 2
D. 3
查看答案和解析>>
科目：初中数学 来源： 题型：
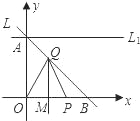
【题目】如图所示，已知直线L过点A（0，1）和B（1，0），P是x轴正半轴上的动点，OP的垂直平分线交L于点Q，交x轴于点M．
（1）直接写出直线L的解析式；
（2）设OP＝t，△OPQ的面积为S，求S关于t的函数关系式；并求出当0＜t＜2时，S的最大值；
（3）直线L1过点A且与x轴平行，问在L1上是否存在点C，使得△CPQ是以Q为直角顶点的等腰直角三角形？若存在，求出点C的坐标，并证明；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
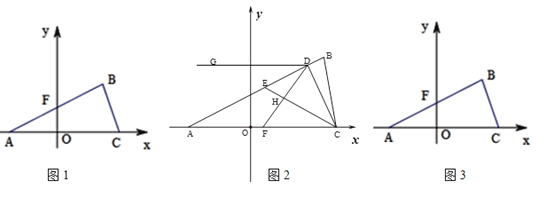
【题目】如图1，在平面直角坐标系中，点A（a，0），B（b，3），C（c，0），满足
+
+
=0．
（1）分别求出点
，
，
的坐标及三角形ABC的面积．
（2）如图2．过点C作
于点D，F是线段AC上一点，满足
，若点G是第二象限内的一点，连接DG，使
，点E是线段AD上一动点（不与A、D重合），连接CE交DF于点H，点E在线段AD上运动的过程中，
的值是否会变化？若不变，请求出它的值；若变化，请说明理由．
（3）如图3，若线段AB与
轴相交于点F，且点F的坐标为（0，
），在坐标轴上是否存在一点P，使三角形ABP和三角形ABC的面积相等？若存在，求出P点坐标．若不存在，请说明理由．（点C除外）
查看答案和解析>>
科目：初中数学 来源： 题型：
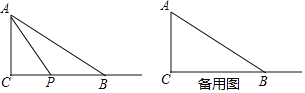
【题目】如图,已知RT△ABC中,∠C=90°，AC=4，BC=8.动点P从点C出发,以每秒2个单位的速度沿射线CB方向运动,连接AP,设运动时间为ts.
（1）求斜边AB的长
（2）当t为何值时,△PAB的面积为6
（3）若t<4,请在所给的图中画出△PAB中AP边上的高BQ，问:当t为何值时,BQ长为4?并求出此时点Q到边BC的距离
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,在平行四边形ABCD中,E、F分别是边AD、BC的中点,AC分别交BE、DF于点M、N.给出下列结论：①△ABM≌△CDN；②AM=
AC；③DN=2NF；④S△AMB=
△ABC；其中正确的结论是______________(只填序号)。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，在下列条件中，不能作为判断△ABD≌△BAC的条件是（ )
A. ∠D＝∠C，∠BAD＝∠ABC B. ∠BAD＝∠ABC，∠ABD＝∠BAC
C. BD＝AC，∠BAD＝∠ABC D. AD＝BC，BD＝AC
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，过点B（6，0）的直线AB与直线OA相交于点A（4，2），动点M在线段OA和射线AC上运动．
（1）求直线AB的解析式．
（2）求△OAC的面积．
（3）是否存在点M，使△OMC的面积是△OAC的面积的
？若存在求出此时点M的坐标；若不存在，说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
