
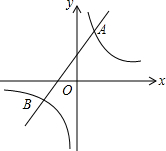
 如图,一次函数y=k1x+b与反比例函数y=$\frac{{k}_{2}}{x}$的图象交于A(2,m),B(-3,-2)两点.
如图,一次函数y=k1x+b与反比例函数y=$\frac{{k}_{2}}{x}$的图象交于A(2,m),B(-3,-2)两点.分析 (1)把B(-3,-2)代入y=$\frac{{k}_{2}}{x}$可得反比例函数的解析式,把点A(2,m)代入即可得到m的值;
(2)根据A(2,3),B(-3,-2),即可得到不等式k1x+b>$\frac{{k}_{2}}{x}$的解集;
(3)分为两种情况:点P在第三象限时,点P在第一象限时,分别根据y1>y2,得到实数p的取值范围.
解答 解(1)把B(-3,-2)代入y=$\frac{{k}_{2}}{x}$得:k2=6,
即反比例函数的解析式是y=$\frac{6}{x}$;
又点A(2,m)在反比例函数y=$\frac{6}{x}$ 图象上,
∴m=3;
(2)∵A(2,3),B(-3,-2),
∴不等式k1x+b>$\frac{{k}_{2}}{x}$的解集是-3<x<0或x>2;
(3)分为两种情况:
当点P在第三象限时,要使y1>y2,实数p的取值范围是p<-2,
当点P在第一象限时,要使y1>y2,实数p的取值范围是p>0.
点评 本题主要考查了反比例函数与一次函数交点问题,解决问题的关键是运用数形结合思想进行求解.解题时注意:反比例函数与一次函数的交点坐标,同时符合两个函数关系式.


科目:初中数学 来源: 题型:解答题
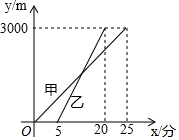 赛龙舟是端午节的主要习俗,某市甲乙两支龙舟队在端午节期间进行划龙舟比赛,从起点A驶向终点B,在整个行程中,龙舟离开起点的距离y(米)与时间x(分钟)的对应关系如图所示,请结合图象解答下列问题:
赛龙舟是端午节的主要习俗,某市甲乙两支龙舟队在端午节期间进行划龙舟比赛,从起点A驶向终点B,在整个行程中,龙舟离开起点的距离y(米)与时间x(分钟)的对应关系如图所示,请结合图象解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
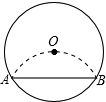 如图将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为( )
如图将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为( )| A. | 2cm | B. | $\sqrt{3}$cm | C. | 2$\sqrt{5}$cm | D. | 2$\sqrt{3}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 下面是一组同学做“抛掷质地均匀的硬币试验”获得的数据.
下面是一组同学做“抛掷质地均匀的硬币试验”获得的数据.| 抛掷次数 | 100 | 200 | 300 | 400 | 500 |
| 正面朝上的 频数m | 51 | 98 | 153 | 200 | 250 |
| 正面朝上的 频率mn | 0.51 | 0.49 | 0.51 | 0.50 | 0.51 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com