
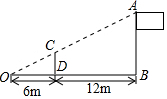
 如图,小明用长为2.5m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿、旗杆的顶端的影子恰好落在地面的同一点O.此时,竹竿与这一点O相距6m、与旗杆相距12m,则旗杆AB的高为7.5m.
如图,小明用长为2.5m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿、旗杆的顶端的影子恰好落在地面的同一点O.此时,竹竿与这一点O相距6m、与旗杆相距12m,则旗杆AB的高为7.5m.  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 工种 | 人数 | 每人每月工资/元 |
| 电工 | 5 | 4000 |
| 木工 | 4 | 3000 |
| 瓦工 | 5 | 2000 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
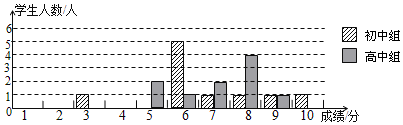
| 组别 | 平均分 | 中位数 | 众数 | 方差 | 优胜奖率 | 优秀奖率 |
| 初中 | 6.7 | 6 | 6 | 3.41 | 90% | 20% |
| 高中 | 7.1 | 7.5 | 8 | 1.69 | 80% | 10% |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
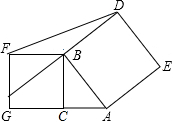 如图所示,在Rt△ABC中,∠ACB=90°,以AB、BC为边向外作正方形ABDE、BCGF,连接DF,且S正方形ABDE=7,S正方形BCGF=3,则△DBF的面积等于$\sqrt{3}$.
如图所示,在Rt△ABC中,∠ACB=90°,以AB、BC为边向外作正方形ABDE、BCGF,连接DF,且S正方形ABDE=7,S正方形BCGF=3,则△DBF的面积等于$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com