
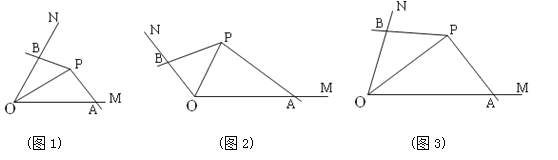
【题目】(定义)如图1,点P为∠MON的平分线上一点,以P为顶点的角的两边分别与射线OM,ON交于A,B两点,如果∠APB绕点P旋转时始终满足![]() ,我们就把∠APB叫做∠MON的智慧角.请利用“智慧角”的定义解决下列两个问题:
,我们就把∠APB叫做∠MON的智慧角.请利用“智慧角”的定义解决下列两个问题:
(运用)(1)如图2,已知∠MON=120°,点P为∠MON的平分线上一点,以点P为顶点的角的两边分别与射线OM,ON交于A,B两点,且∠APB=120°.求证:∠APB是∠MON的智慧角.
(探究)(2)如图3,已知∠MON=![]() (0°<
(0°<![]() <90°),OP=4,若∠APB是∠MON的智慧角,连接AB,试用含
<90°),OP=4,若∠APB是∠MON的智慧角,连接AB,试用含![]() 的代数式分别表示∠APB的度数和△AOB的面积.
的代数式分别表示∠APB的度数和△AOB的面积.
【答案】(1)证明见解析;(2)∠APB=180°-![]() α,
α,![]()
【解析】
(1)由角平分线求出∠AOP=∠BOP=![]() ∠MON=60°,再证出∠OAP=∠OPB,证明△AOP∽△POB,得出对应边成比例
∠MON=60°,再证出∠OAP=∠OPB,证明△AOP∽△POB,得出对应边成比例![]() ,得出OP2=OAOB,即可得出结论;
,得出OP2=OAOB,即可得出结论;
(2)由∠APB是∠MON的智慧角,得出![]() ,证出△AOP∽△POB,得出对应角相等∠OAP=∠OPB,即可得出∠APB=180°-
,证出△AOP∽△POB,得出对应角相等∠OAP=∠OPB,即可得出∠APB=180°-![]() α;过点A作AH⊥OB于H,由三角形的面积公式得出:S△AOB=
α;过点A作AH⊥OB于H,由三角形的面积公式得出:S△AOB=![]() OBAH,即可得出S△AOB=8sinα.
OBAH,即可得出S△AOB=8sinα.
运用(1)证明:
∵∠MON=120°,点P为∠MON的平分线上一点,
∴![]() .
.
∵∠AOP+∠OAP+∠APO=180°,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴∠OAP=∠OPB.
∴△AOP∽△POB.
∴![]() ,即OP2=OA·OB,∴∠APB是∠MON的智慧角.
,即OP2=OA·OB,∴∠APB是∠MON的智慧角.
探究(2)∵∠APB是∠MON的智慧角,
∴OP2=OA·OB,即![]() .
.
∵点P为∠MON的平分线上一点,
∴![]()
![]()
∴△AOP∽△POB.
∴∠OAP=∠OPB.
∴∠APB=∠OPB+∠OPA=∠OAP+∠OPA=180°-![]()
如图,过点A作AH⊥OB于点H,

∴SAOB=![]() .
.
∵OP=4,∴![]() .
.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】国家为了实现2020年全面脱贫目标,实施“精准扶贫”战略,采取异地搬迁,产业扶持等措施.使贫困户的生活条件得到改善,生活质量明显提高.某旗县为了全面了解贫困县对扶贫工作的满意度情况,进行随机抽样调查,分为四个类别:A.非常满意;B.满意;C.基本满意;D.不满意.依据调查数据绘制成图1和图2的统计图(不完整).
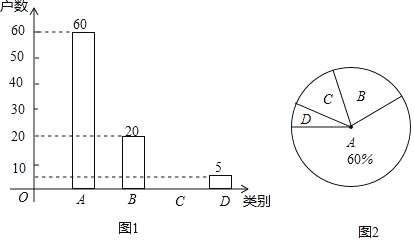
根据以上信息,解答下列问题:
(1)将图1补充完整;
(2)通过分析,贫困户对扶贫工作的满意度(A、B、C类视为满意)是 ;
(3)市扶贫办从该旗县甲乡镇3户、乙乡镇2户共5户贫困户中,随机抽取两户进行满意度回访,求这两户贫困户恰好都是同一乡镇的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),抛物线与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论

①a-b+c>0;②3a+b=0;
③b2=4a(c-n);
④一元二次方程ax2+bx+c=n-1有两个不相等的实数根.
其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
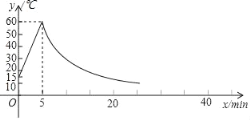
【题目】制作一种产品,需先将材料加热达到60℃后,再进行操作,设该材料温度为y(℃)从加热开始计算的时间为x(min).据了解,当该材料加热时,温度y与时间x成一次函数关系:停止加热进行操作时,温度y与时间x成反比例关系(如图).已知在操作加热前的温度为15℃,加热5分钟后温度达到60℃.
(1)分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;
(2)根据工艺要求,当材料的温度低于15℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
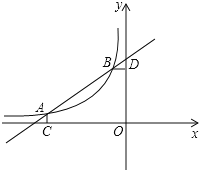
【题目】如图,已知A(﹣4,![]() ),B(﹣1,n)是一次函数y=kx+b与反比例函数y=
),B(﹣1,n)是一次函数y=kx+b与反比例函数y=![]() (m≠0,m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
(m≠0,m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
(1)求一次函数解析式及m的值;
(2)根据图象直接写出在第二象限内,当x取何值时,一次函数小于于反比例函数的值?
(3)P是线段AB上的一点,连接PC,PD,若△PCA和△PDB面积相等,求点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,某校举办了学生“国学经典大赛”.比赛项目为:A.唐诗;B.宋词;C.论语;D.三字经.比赛形式为“单人组”和“双人组”.小红和小明组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次,则恰好小红抽中“唐诗”且小明抽中“宋词”的概率是多少?请用画树状图或列表的方法进行说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个梯子AB斜靠在一竖直的墙AO上,测得AO=2 m.若梯子的顶端沿墙下滑0.5米,这时梯子的底端也恰好外移0.5米,则梯子的长度AB为( )
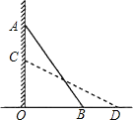
A. 2.5 m B. 3 m C. 1.5 m D. 3.5 m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x与双曲线y=
x与双曲线y=![]() (x>0)交于点A,将直线y=
(x>0)交于点A,将直线y=![]() x向右平移3个单位后,与双曲线y=
x向右平移3个单位后,与双曲线y=![]() (x>0)交于点B,与x轴交于点C,若
(x>0)交于点B,与x轴交于点C,若![]() =2,则k=( )
=2,则k=( )

A. ![]() B. 4 C. 6 D.
B. 4 C. 6 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
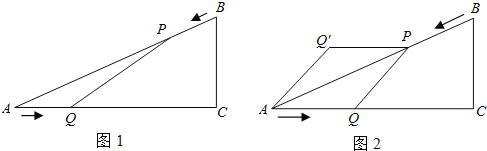
【题目】如图1,已知△ABC中,AB=10cm,AC=8cm,BC=6 cm ,如果点P由B出发沿BA方向向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm /s,连接PQ,设运动的时间为t(单位:s)(0≤t≤4).解答下列问题:
(1)当t为何值时,PQ∥BC.
(2)是否存在某时刻t,使线段PQ恰好把△ABC的面积平分?若存在求出此时t的值;若不存在,请说明理由.
(3)如图2,把△APQ沿AP翻折,得到四边形AQPQ′.那么是否存在某时刻t使四边形AQPQ′为菱形?若存在,求出此时菱形的面积;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com