
分析 设快车的速度为xm/s,慢车的速度为ym/s,根据从两车车头相遇到车尾离开共需13秒钟,快车从后面追慢车,从快车车头追上慢车车尾到快车车尾离开慢车车头共需65秒,列方程组求解.
解答 解:设快车的速度为xm/s,慢车的速度为ym/s,依题意有
$\left\{\begin{array}{l}{13(x+y)=306+344}\\{65(x-y)=306+344}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=30}\\{y=20}\end{array}\right.$.
答:快车的速度为30m/s,慢车的速度为20m/s.
点评 本题考查了二元一次方程组的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程组求解.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AB∥CD,直线EF分别交AB、CD于点E、F,HF平分∠EFD,若∠1=110°,则∠2的度数为( )
如图,AB∥CD,直线EF分别交AB、CD于点E、F,HF平分∠EFD,若∠1=110°,则∠2的度数为( )| A. | 55° | B. | 40° | C. | 35° | D. | 45° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
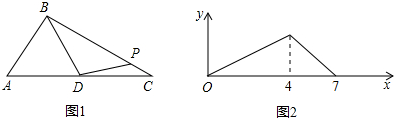
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
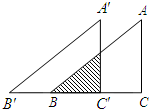 如图,△ABC≌△A′B′C′,∠C=∠C′=90°,AC=3cm,A′B′=5cm,先将△ABC和△A′B′C′完全重合,再将△ABC固定,△A′B′C′沿CB所在的直线向左以每秒1cm的速度平行移动,3秒后重叠部分的面积为$\frac{3}{8}$cm2.
如图,△ABC≌△A′B′C′,∠C=∠C′=90°,AC=3cm,A′B′=5cm,先将△ABC和△A′B′C′完全重合,再将△ABC固定,△A′B′C′沿CB所在的直线向左以每秒1cm的速度平行移动,3秒后重叠部分的面积为$\frac{3}{8}$cm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
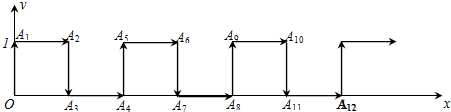
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
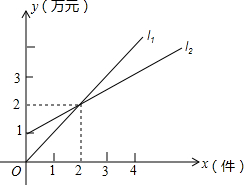 如图,l1表示某个公司一种产品一天的销售收入与销售量的关系,l2表示该公司这种产品一天的销售成本与销售量的关系.
如图,l1表示某个公司一种产品一天的销售收入与销售量的关系,l2表示该公司这种产品一天的销售成本与销售量的关系.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com