
【题目】已知,如图,A、B分别为数轴上的两点,A点对应的数为-20,B点对应的数为100.
![]()
请写出AB中点M对应的数。
(2)现有一只电子蚂蚁P从B点出发,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度向右运动。设两只电子蚂蚁在数轴上的C点相遇,你知道C点对应的数是多少吗?
(3)若当电子蚂蚁P从B点出发时,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度也向左运动。设两只电子蚂蚁在数轴上的D点相遇,你知道D点对应的数是多少吗?
【答案】(1)40; (2)28;(3)﹣260.
【解析】(1)求-20与100和的一半即是M;
(2)此题是相遇问题,先求出相遇所需的时间,再求出点Q走的路程,根据左减右加的原则,可求出-20向右运动到相遇地点所对应的数;
(3)此题是追及问题,可先求出P追上Q所需的时间,然后可求出Q所走的路程,根据左减右加的原则,可求出点D所对应的数.
解:(1)∵A、B分别为数轴上的两点,A点对应的数为-20,B点对应的数为100,
∴![]() =60;
=60;
则AB中点M对应的数是100-60=40;
(2)它们的相遇时间是120÷(6+4)=12,
即相同时间Q点运动路程为:12×4=48,
即从数﹣20向右运动48个单位到数28;
(3)P点追到Q点的时间为120÷(6﹣4)=60,
即此时Q点运动的路程为4×60=240,
即从数﹣20向左运动240个单位到数﹣260.
“点睛”此题考查的是数轴上点的运动,熟知数轴上两点间距离的定义是解答此题的关键.还有相遇问题与追及问题.注意用到了路程=速度×时间.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
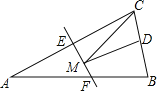
【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点,若点D为BC边的中点,点M为线段EF上一动点,则![]() 周长的最小值为______.
周长的最小值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数分别填入相应的集合里.
-4,![]() ,0,
,0,![]() ,-3.14,717,-(+5),+1.88,
,-3.14,717,-(+5),+1.88,![]()
(1)正数集合:{ … };
(2)负数集合:{ …};
(3)整数集合:{ …};
(4)分数集合:{ … }.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC是等边三角形,点D、E分别在BC,AC且BD=CE,AD、BE相交于点M,

求证:(1)△AME∽△BAE;(2)BD2=AD×DM.
查看答案和解析>>
科目:初中数学 来源: 题型:
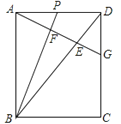
【题目】如图,在长方形![]() 中,
中, ![]() 是
是![]() 边上一动点,连接
边上一动点,连接![]() ,过点
,过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
(1)当![]() =
=![]() ,且
,且![]() 是
是![]() 的中点时,求证:
的中点时,求证: ![]() =
=![]() .
.
(2)在(1)的条件下,求![]() 的值;
的值;
(3)类比探究:若![]() =3
=3![]() ,
, ![]() =2
=2![]() ,则
,则![]() = .
= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠![]() =90°,
=90°,![]() =
=![]() =6,点
=6,点![]() 在边
在边![]() 上运动,过点
上运动,过点![]() 作
作![]() ⊥
⊥![]() 于点
于点![]() ,以
,以![]() 、
、![]() 为邻边作□
为邻边作□![]() ,设□
,设□![]() 与△
与△![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() ,线段
,线段![]() 的长为
的长为![]() (0<
(0<![]() ≤6).
≤6).
(1)求线段![]() 的长(用含
的长(用含![]() 的代数式表示)
的代数式表示)
(2)当点![]() 落现在变
落现在变![]() 上时,求
上时,求![]() 的值;
的值;
(3)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(4)直接写出点![]() 到△
到△![]() 任意两边所在直线的距离相等时
任意两边所在直线的距离相等时![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请根据图中提供的信息,列一元一次方程解应用题,回答下列问题:
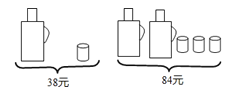
(1)求一个暖瓶与一个水杯分别是多少元?
(2)若买3个暖瓶与4个水杯一共需要多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对
他们进行了六次测试,测试成绩如下表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 |
(1)根据表格中的数据,计算出甲的平均成绩是 环,乙的平均成绩是 环;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1)、(2)计算的结果,你认为推荐谁参加全国比赛更合适,请说明理由.
(计算方差的公式:s2=![]() [
[![]() ])
])
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:某校组织七年级师生共300人乘车前往“故乡”农场进行劳动教育活动.
(1)他们早晨8:00从学校出发,原计划当天上午10:00便可以到达“故乡”农场,但实际上他们当天上午9:40便达到了“故乡”农场,已知汽车实际行驶速度比原计划行驶速度快10km/h.求汽车原计划行驶的速度.
(2)到达“故乡”农场后,需要购买门票,已知该农场门票票价情况如右表,该校购买门票时共花了3100元,那么参加此次劳动教育的教师、学生各多少人?
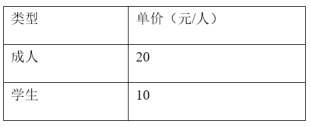
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com