
 如图,若△ABC与△BCD都是直角三角形,∠BDC=∠BAC=Rt∠.点E是BC的中点,连接DE、AE、AD,求证:△ADE是等腰三角形.
如图,若△ABC与△BCD都是直角三角形,∠BDC=∠BAC=Rt∠.点E是BC的中点,连接DE、AE、AD,求证:△ADE是等腰三角形. 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:阅读理解
| BF | CD |

查看答案和解析>>
科目:初中数学 来源:2013年江苏省南京市玄武区中考一模数学试卷(带解析) 题型:单选题
如图,若△ABC与△A'B'C'关于直线MN对称,BB'交MN于点O,则下列说法中不一定正确的是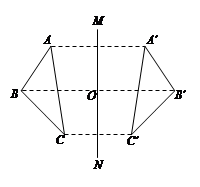
| A.AC=A'C' |
| B.AB∥B'C' |
| C.AA'⊥MN |
| D.BO=B'O |
查看答案和解析>>
科目:初中数学 来源:2013-2014学年辽宁鞍山第26中学九年级上学期第三次月考数学试卷(解析版) 题型:解答题
阅读材料

如图①,△ABC与△DEF都是等腰直角三角形,ACB=∠EDF=90°,且点D在AB边上,AB、EF的中点均为O,连结BF、CD、CO,显然点C、F、O在同一条直线上,可以证明△BOF≌△COD,则BF=CD.解决问题:
(1)将图①中的Rt△DEF绕点O旋转得到图②,猜想此时线段BF与CD的数量关系,并证明你的结论;
(2)如图③,若△ABC与△DEF都是等边三角形,AB、EF的中点均为O,上述(1)中的结论仍然成立吗?如果成立,请说明理由;如不成立,请求出BF与CD之间的数量关系;
(3)如图④,若△ABC与△DEF都是等腰三角形,AB、EF的中点均为0,且顶角∠ACB=∠EDF=α,请直接写出 的值(用含α的式子表示出来)
的值(用含α的式子表示出来)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com