
【题目】类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.
(1)概念理解
如图1,在四边形ABCD中,添加一个条件使得四边形ABCD是“等邻边四边形”.请写出你添加的一个条件.
(2)问题探究
①小红猜想:对角线互相平分的“等邻边四边形”是菱形.她的猜想正确吗?请说明理由。
②如图2,小红画了一个Rt△ABC,其中∠ABC=90°,AB=2,BC=1,并将Rt△ABC沿
∠ABC的平分线BB'方向平移得到△A'B'C',连结AA',BC'.小红要是平移后的四边形ABC'A'是“等邻边四边形”,应平移多少距离(即线段BB'的长)?

【答案】(1)AB=BC或BC=CD或CD=AD或AD=AB(任写一个即可);
【解析】(1)由“等邻边四边形”的定义易得出结论;(2)①正确,②2; ![]()
![]()
![]() .
.
(2)①先利用平行四边形的判定定理得平行四边形,再利用“等邻边四边形”定义得邻边相等,得出结论;
②由平移的性质易得BB′=AA′,A′B′∥AB,A′B′=AB=2,B′C′=BC=1,A′C′=AC=![]() ,再利用“等邻边四边形”定义分类讨论,由勾股定理得出结论;
,再利用“等邻边四边形”定义分类讨论,由勾股定理得出结论;
解:(1)AB=BC或BC=CD或CD=AD或AD=AB(任写一个即可);
(2)①正确,理由为:
∵四边形的对角线互相平分,∴这个四边形是平行四边形,
∵四边形是“等邻边四边形”,∴这个四边形有一组邻边相等,
∴这个“等邻边四边形”是菱形;
②∵∠ABC=90°,AB=2,BC=1,
∴AC=![]() ,
,
∵将Rt△ABC平移得到△A′B′C′,
∴BB′=AA′,A′B′∥AB,A′B′=AB=2,B′C′=BC=1,A′C′=AC=![]() ,
,
(I)如图1,当AA′=AB时,BB′=AA′=AB=2;

(II)如图2,当AA′=A′C′时,BB′=AA′=A′C′=![]() ;
;

(III)当A′C′=BC′=![]() 时,
时,
如图3,延长C′B′交AB于点D,则C′B′⊥AB,

∵BB′平分∠ABC,
∴∠ABB′=![]() ∠ABC=45°,
∠ABC=45°,
∴∠BB′D=′∠ABB′=45°,
∴B′D=B,
设B′D=BD=x,
则C′D=x+1,BB′=![]() x,
x,
∵在Rt△BC′D中,BD2+(C′D)2=(BC′)2
∴x2+(x+1)2=(![]() )2,
)2,
解得:x1=1,x2=﹣2(不合题意,舍去),
∴BB′=![]() x=
x=![]() ,
,
(Ⅳ)当BC′=AB=2时,如图4,

与(Ⅲ)方法一同理可得:BD2+(C′D)2=(BC′)2,
设B′D=BD=x,
则x2+(x+1)2=22,
解得:x1=![]() ,x2=
,x2=![]() (不合题意,舍去),
(不合题意,舍去),
∴BB′=![]() x=
x=![]() ;
;
“点睛”本题主要考查了对新定义的理解,菱形的判定,勾股定理等,理解新定义,分类讨论是解答此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列等式由左边向右边的变形中,属于因式分解的是 ( )
A.x2+5x-1=x(x+5)-1B.x2-4+3x=(x+2)(x-2)+3x
C.(x+2)(x-2)=x2-4D.x2-9=(x+3)(x-3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在等边三角形ABC中.D是AB边上的动点,以CD为一边,向上作等边三角形EDC.连接AE.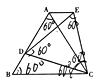
(1)求证:△DBC≌△EAC
(2)试说明AE∥BC的理由.
(3)如图②,当图①中动点D运动到边BA的延长线上时,所作仍为等边三角形,猜想是否仍有AE∥BC?若成立请证明.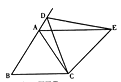
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进一批单价为20元的日用品,如果以单价30元销售,那么半个月内可以售出400件.根据销售经验,提高单价会导致销售量的减少,即销售单价每提高1元,销售量相应减少20件.如果售价为x元,总利润为y元。
(1)写出y与x的函数关系式
(2)当售价x为多少元时,总利润为y最大,最大值是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,∠C=90,AC<BC,D为BC上一点,且到A,B两点的距离相等.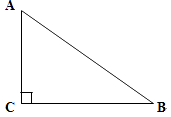
(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);
(2)连结AD,若∠B=37°,则∠CAD=度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-(2k+1)x+4(k-0.5)=0
(1)判断方程根的情况;
(2)k为何值时,方程有两个相等的实数根,并求出此时方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.任意抛掷一枚质地均匀的硬币10次,则“有5次正面朝上”是必然事件
B.明天的降水概率为40%,则“明天下雨”是确定事件
C.篮球队员在罚球线上投篮一次,则“投中”是随机事件
D.a是实数,则“|a|≥0”是不可能事件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com