
【题目】为了贯彻教育部关于中小学生“每天锻炼一小时”的要求,某市教育局做了一次随机抽样调查,其内容是:(1)学生每天锻炼时间是否达到1小时;(2)学生每天锻炼时间未达到1小时的原因.随机调查了600名学生,把所得的数据制成了如下的扇形统计图和条形统计图(不完整)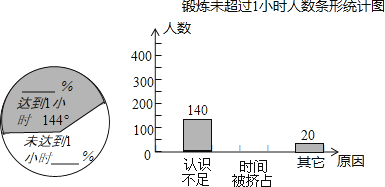
根据图示,回答以下问题:
(1)每天锻炼时间达到1小时的人数占被调查总人数的百分比是;
每天锻炼时间未达到1小时的人数占被调查总人数的百分比是;
每天锻炼时间未达到1小时的人数为人,其中原因是“时间被挤占”的人数是人;
(2)补全扇形统计图和条形统计图;
(3)若该市现有中小学生约27万人,据此调查,可估计今年该市中小学生每天锻炼未达到1小时的学生约有多少万人?
(4)从这次接受调查的学生中,随机抽取一名学生的“每天锻炼一小时”的情况,回答内容为“时间被挤占”的概率是多少?
【答案】
(1)40%;60%;360;200
(2)
解:补全统计图如图
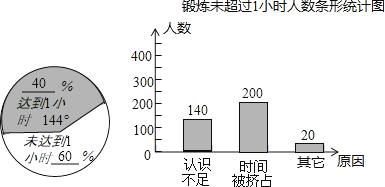
(3)
解:27×60%=16.2万人
(4)
解:P(时间被挤占)= 200 600 = 1 3 .
【解析】解:(1)达到1小时的人数占被调查总人数的百分比: ![]() ×100°=40%,
×100°=40%,
未达到1小时的人数占被调查总人数的百分比:1﹣40%=60%,
未达到1小时的人数:600×60%=360人,其中原因是“时间被挤占”的人数:360﹣140﹣20=200人;
所以答案是:40%,60%,360,200;
(1)用144°除以360°计算即可求出达到1小时的人数的百分比;
根据两部分所占的百分比之和为1计算即可求出未达到1小时的人数所占的百分比;
用所求的百分比乘以600,计算即可求出未达到1小时的人数,再根据条形统计图求出时间被挤占的人数;(2)根据(1)的计算补全统计图即可;(3)用总人数27万乘以“未达到1小时的学生”所占的百分比,计算即可得解;(4)用回答时间被挤占的人数除以接受调查的人数,计算即可得解.
【考点精析】认真审题,首先需要了解扇形统计图(能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况),还要掌握条形统计图(能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】正方形ABCD与正五边形EFGHM的边长相等,初始如图所示,将正方形绕点F顺时针旋转使得BC与FG重合,再将正方形绕点G顺时针旋转使得CD与GH重合…按这样的方式将正方形依次绕点H、M、E旋转后,正方形中与EF重合的是( )
A.AB
B.BC
C.CD
D.DA
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,BE平分∠ABC,CF平分∠BCD,BE、CF交于点G.若使EF= ![]() AD,那么平行四边形ABCD应满足的条件是( )
AD,那么平行四边形ABCD应满足的条件是( )
A.∠ABC=60°
B.AB:BC=1:4
C.AB:BC=5:2
D.AB:BC=5:8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在纸面上有一数轴(如图),折叠纸面.
(1)若表示﹣1的点与表示3的点重合,回答以下问题:
①表示5的点与表示数_________的点重合;
②若数轴上A、B两点之间的距离为9(A在B的左侧),且A、B两点经折叠后重合,求A、B两点表示的数是多少?
(2)若点D表示的数为x,则当x为_______时,|x+1|与|x﹣2|的值相等.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农户承包果树若干亩,今年投资![]() 元,收获水果总产量为
元,收获水果总产量为![]() 千克.此水果在市场上每千克售
千克.此水果在市场上每千克售![]() 元,在果园直接销售每千克售
元,在果园直接销售每千克售![]() 元
元![]() .该农户将水果拉到市场出售平均每天出售
.该农户将水果拉到市场出售平均每天出售![]() 千克,需
千克,需![]() 人帮忙,每人每天付工资
人帮忙,每人每天付工资![]() 元,农用车运费及其他各项税费平均每天
元,农用车运费及其他各项税费平均每天![]() 元.
元.
![]() 分别用含
分别用含![]() ,
,![]() 的代数式表示两种方式出售水果的收入.
的代数式表示两种方式出售水果的收入.
![]() 若
若![]() 元,
元,![]() 元,且两种出售水果方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好.
元,且两种出售水果方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好.
![]() 该农户加强果园管理,力争到明年纯收入达到
该农户加强果园管理,力争到明年纯收入达到![]() 元,而且该农户采用了
元,而且该农户采用了![]() 中较好的出售方式出售,那么纯收入增长率是多少(纯收入
中较好的出售方式出售,那么纯收入增长率是多少(纯收入![]() 总收入-总支出)?
总收入-总支出)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上(E不与A、B重合),连接EF、CF,则下列结论中一定成立的是 ( )
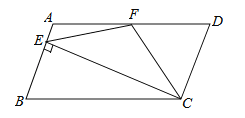
①∠DCF=![]() ∠BCD;②EF=CF;③
∠BCD;②EF=CF;③![]() ;④∠DFE=4∠AEF.
;④∠DFE=4∠AEF.
A. ①②③④ B. ①②③ C. ①② D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】福鼎市南溪水库的警戒水位是![]() ,以下是南溪水库管理处七月份某周监测到的水位变化情况,上周末恰好达到警戒水位(正数表示比前一天水位高,负数表示比前一天水位低).
,以下是南溪水库管理处七月份某周监测到的水位变化情况,上周末恰好达到警戒水位(正数表示比前一天水位高,负数表示比前一天水位低).
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
水位变化 |
|
|
|
|
|
|
|

![]() 星期四的水位是多少?
星期四的水位是多少?
![]() 从这周一到周日哪天的水位是最高的?
从这周一到周日哪天的水位是最高的?
![]() 以警戒水位为零点,用折线图表表示本周水位情况.
以警戒水位为零点,用折线图表表示本周水位情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般情况下![]() 不成立,但有些数可以使得它成立,例如:m=n=0时,我们称使得
不成立,但有些数可以使得它成立,例如:m=n=0时,我们称使得![]() 成立的一对数m,n为“相伴数对”,记为(m,n).
成立的一对数m,n为“相伴数对”,记为(m,n).
(1)若(m,1)是“相伴数对”,则m=_____;
(2)(m,n)是“相伴数对”,则代数式![]() m﹣[n+
m﹣[n+![]() (6﹣12n﹣15m)]的值为_____.
(6﹣12n﹣15m)]的值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com