
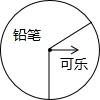
 如图,某商场设立了一个可以自由转动的转盘,并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.表是活动进行中的一组统计数据:
如图,某商场设立了一个可以自由转动的转盘,并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.表是活动进行中的一组统计数据:| 转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 落在“铅笔”的次数m | 68 | 111 | 136 | 345 | 564 | 701 |
| 落在“铅笔”的频率$\frac{m}{n}$ | 0.68 | 0.74 | 0.68 | 0.69 | 0.71 | 0.70 |
分析 (1)分别利用表格中数据结合频率公式求出即可;
(2)利用(1)中所求频率即可估计出当n很大时,频率将会接近的值;
(3)利用(2)中所求可得出落在“铅笔”的概率,进而得出落在“可乐”的概率.
解答 解:(1)填表如下:
| 转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 落在“铅笔”的次数m | 68 | 111 | 136 | 345 | 564 | 701 |
| 落在“铅笔”的频率$\frac{m}{n}$ | 0.68 | 0.74 | 0.68 | 0.69 | 0.71 | 0.70 |
点评 此题主要考查了频率求法以及利用频率估计概率,正确理解频率与概率之间的关系是解题关键.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{100}$ | B. | -$\frac{1}{100}$ | C. | $\frac{25}{144}$ | D. | $\frac{25}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com