
【题目】如图:E在线段CD上,EA、EB分别平分∠DAB和∠CBA,∠AEB=90°,设AD=![]() ,BC=
,BC=![]() ,且
,且![]() .
.
(1)求AD和BC的长;
(2)你认为AD和BC还有什么关系?并验证你的结论;
(3)取AB中点F,连接EF,且EF∥AD∥BC。若EF=![]() ,你能求出AB的长度吗?若能,请写出推理过程;若不能,请说明理由.
,你能求出AB的长度吗?若能,请写出推理过程;若不能,请说明理由.
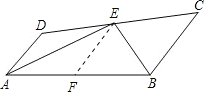
【答案】(1)AD=3,BC=4;(2)AD∥BC,理由见解析;(3)能.7.
【解析】分析:(1)根据题意可知x-3=0,y-4=0,易求解AD和BC的长;(2)根据∠AEB=90°,可得∠EAB+∠EBA=90°,因为EA、EB分别平分∠DAB和∠CBA,则∠DAB+∠ABC=180°,所以AD∥BC;(3)如图,过E作EF∥AD,交AB于F,则∠DAE=∠AEF,∠EBC=∠BEF,因为EA、EB分别平分∠DAB和∠CBA,所以AF=EF=FB,再根据梯形中位线定理易求AB的长.
详解:(1)∵AD=x,BC=y,且(x﹣3)2+|y﹣4|=0,∴AD=3,BC=4.
(2)AD∥BC,
理由是:∵在△AEB中,∠AEB=90°,∴∠EAB+∠EBA=90°,
又∵EA、EB分别平分∠DAB和∠CBA,∴∠DAB+∠ABC=180°.
∴AD∥BC.
(3)能.
如图,
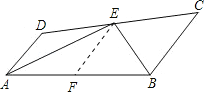
∵AD∥EF∥BC,则∠DAE=∠AEF,∠EBC=∠BEF,
∵EA、EB分别平分∠DAB和∠CBA,
∴∠EAF=∠AEF,∠EBF=∠BEF,
∴AF=EF=FB,又∵EF=![]() ,
,
∴AB=7.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】营市公交公司将淘汰所有线路上“冒黑烟”较严重的公交车,计划购买A型和B型两种环保节能公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在该线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1220万元,且确保这10辆公交车在该线路的年均载客总和不少于650万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】5月16日,我校进行了全校师生防灾减灾大演练,警报拉响后同学们匀速跑步到操场,在操场指定位置清点人数、听广播后,再沿原路匀速步行回教室,同学们离开教学楼的距离y与时间x的关系的大致图象是( )
A.  B.
B.  C.
C.  D.
D. 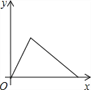
查看答案和解析>>
科目:初中数学 来源: 题型:
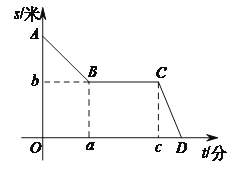
【题目】李老师为锻炼身体一直坚持步行上下班.已知学校到李老师家总路程为2000米.一天,李老师下班后,以45米/分的速度从学校往家走,走到离学校900米时,正好遇到一个朋友,停下又聊了半小时,之后以110米/分的速度走回了家.李老师回家过程中,离家的路程s(米)与所用时间t(分)之间的关系如图所示.
(1)求a,b,c的值;
(2)求李老师从学校到家的总时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个芭蕾舞团参加舞剧《天鹅湖》的表演,已知甲、乙两个团的女演员的身高平均数分别为165cm、165cm,方差分别为S甲2=1.5、S乙2=2.5,则身高更整齐的芭蕾舞团是_____团.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购买60件A商品和30件B商品共用了1080元,购买50件A商品和20件B商品共用了880元.
(1)A、B两种商品的单价分别是多少元?
(2)已知该商店购买B商品的件数比购买A商品的件数的2倍少4件,如果需要购买A、B两种商品的总件数不少于32件,且该商店购买的A、B两种商品的总费用不超过296元,那么该商店有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对数轴上的点P进行如下操作:先把点P表示的数乘以![]() ,再把所得数对应的点向右平移1个单位,得到点P的对应点P′,点A,B在数轴上,对线段AB上的每个点进行上述操作后得到线段A′B′,其中点A,B的对应点分别为A′,B′,如图,若点A表示的数是﹣3,则点A′表示的数是__;若点B′表示的数是2,则点B表示的数是__.已知线段AB上的点E经过上述操作后得到的对应点E′与点E重合,则点E表示的数是__.
,再把所得数对应的点向右平移1个单位,得到点P的对应点P′,点A,B在数轴上,对线段AB上的每个点进行上述操作后得到线段A′B′,其中点A,B的对应点分别为A′,B′,如图,若点A表示的数是﹣3,则点A′表示的数是__;若点B′表示的数是2,则点B表示的数是__.已知线段AB上的点E经过上述操作后得到的对应点E′与点E重合,则点E表示的数是__.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com