Question

如图1，在Rt△ABC中，∠ACB=90°，∠A=30°，P为BC边上任意一点，点Q为AC边动点，分别以CP、PQ为边做等边△PCF和等边△PQE，连接EF．
（1）试探索EF与AB位置关系，并证明；
（2）如图2，当点P为BC延长线上任意一点时，（1）结论是否成立？请说明理由．
（3）如图3，在Rt△ABC中，∠ACB=90°，∠A=m°，P为BC延长线上一点，点Q为AC边动点，分别以CP、PQ为腰做等腰△PCF和等腰△PQE，使得PC=PF，PQ=PE，连接EF．要使（1）的结论依然成立，则需要添加怎样的条件？为什么？

Answer 1

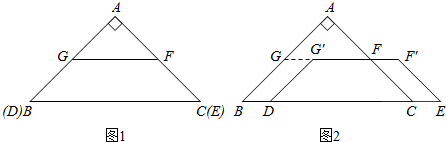
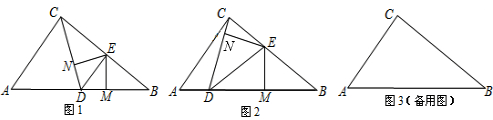
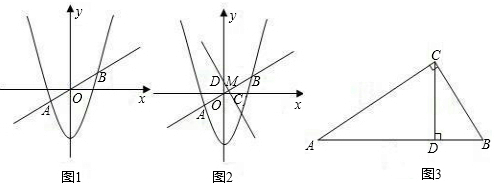
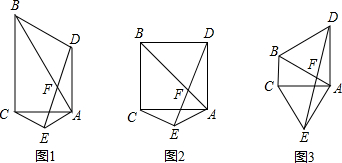
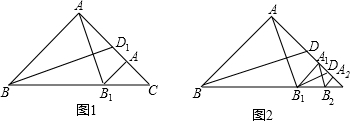
解：（1）EF⊥AB．
证明：∵△PCF和△PQE都是等边三角形，
∴PF=PC，PE=PQ，
∠EPF+∠FPQ=∠QPC+∠FPQ=60°，
∴∠EPF=∠QPC，
在△PFE和△PCQ中

∴△PFE≌△PCQ（SAS）；
∴∠EFP=∠QCP=90°，
∴EF⊥PF；
在Rt△ABC中，∠ACB=90°，∠A=30°，
∴∠B=60°；
又∵∠FPC=60°，
∴∠B=∠FPC，
∴PF∥AB（同位角相等，两直线平行），
∴EF⊥AB；

（2）当点P为BC延长线上任意一点时，（1）结论成立．
证明：∵△PCF和△PQE都是等边三角形，
∴PF=PC，PE=PQ，
∠EPF+∠EPC=∠QPC+∠EPC=60°，
∴∠EPF=∠QPC，
在△PFE和△PCQ中

∴△PFE≌△PCQ（SAS）；
∴∠EFP=∠QCP=90°，
∴EF⊥PF；
在Rt△ABC中，∠ACB=90°，∠A=30°，
∴∠B=60°；
又∵∠FPC=60°，
∴∠B=∠FPC，
∴PF∥AB（内错角相等，两直线平行），
∴EF⊥AB；

（3）要使（1）的结论依然成立，则需要添加条件是：∠CPF=∠B=∠QPE．
需要证明△PFE≌△PCQ、PF∥AB（内错角相等，两直线平行），才能证明EF⊥AB．
分析：（1）通过等边三角形的性质（三条边相等、三个角相等）求得PF=PC，PE=PQ，∠EPF=∠QPC；然后根据全等三角形的判定定理SAS证明△PFE≌△PCQ，再根据全等三角形的性质（对应角相等）知∠EPF=∠QPC=90°；接下来由平行线的判定定理（同位角相等，两直线平行）知PF∥AB；最后由平行线的性质（两平行线中，有一条垂直于第三条直线，则另一条也垂直于第三条直线）知EF⊥AB；
（2）通过等边三角形的性质（三条边相等、三个角相等）求得PF=PC，PE=PQ，∠EPF=∠QPC；然后根据全等三角形的判定定理SAS证明△PFE≌△PCQ，再根据全等三角形的性质（对应角相等）知∠EPF=∠QPC=90°；接下来由平行线的判定定理（内错角相等，两直线平行）知PF∥AB；最后由平行线的性质（两平行线中，有一条垂直于第三条直线，则另一条也垂直于第三条直线）知EF⊥AB；
（3）需要添加的条件需满足：△PFE≌△PCQ、PF∥AB（内错角相等，两直线平行）．
点评：本题综合考查了全等三角形的性质、全等三角形的判定与性质．解答本题要充分利用等边三角形的三边关系、三角关系，可有助于提高解题速度和准确率．