
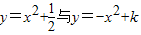 的图象的顶点重合,则下列结论不正确的是( )
的图象的顶点重合,则下列结论不正确的是( )
 的顶点坐标为(0,
的顶点坐标为(0, ),由于二次函数
),由于二次函数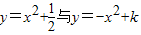 的图象的顶点重合,则得到k=
的图象的顶点重合,则得到k= ,然后根据二次函数性质得到它们的对称轴都为y轴,其中抛物线y=x2+
,然后根据二次函数性质得到它们的对称轴都为y轴,其中抛物线y=x2+ 的开口向上,抛物线y=-x2+
的开口向上,抛物线y=-x2+ 的开口向下,二次函数y=-x2+
的开口向下,二次函数y=-x2+ 的最大值为
的最大值为 ,并且k=
,并且k= 时,可得到方程-x2+k=0有实数根.
时,可得到方程-x2+k=0有实数根. 的顶点坐标为(0,
的顶点坐标为(0, ),
), ),即有k=
),即有k= ,
, 的开口向上,抛物线y=-x2+
的开口向上,抛物线y=-x2+ 的开口向下,二次函数y=-x2+
的开口向下,二次函数y=-x2+ 的最大值为
的最大值为 ,方程-x2+k=0有实数根.
,方程-x2+k=0有实数根.

科目:初中数学 来源: 题型:
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
查看答案和解析>>
科目:初中数学 来源: 题型:044
某校研究性学习小组在研究有关二次函数及其图象的性质的问题时,发现了两个重要结论:一是发现抛物线![]() 当实数a变化时,它的顶点都在某条直线上;二是发现当实数a变化时,若把抛物线
当实数a变化时,它的顶点都在某条直线上;二是发现当实数a变化时,若把抛物线![]() 的顶点的横坐标减少
的顶点的横坐标减少![]() ,纵坐标增加
,纵坐标增加![]() ,得到A点的坐标,若把顶点的横坐标增加
,得到A点的坐标,若把顶点的横坐标增加![]() ,纵坐标增加
,纵坐标增加![]() ,得到B点的坐标,则A、B两点一定仍在抛物线
,得到B点的坐标,则A、B两点一定仍在抛物线![]() 上.
上.
(1)请你协助探求出当实数a变化时,抛物线![]() 的顶点所在直线的解析式;
的顶点所在直线的解析式;
(2)问题(1)中的直线上有一个点不是该抛物线的顶点,你能找出它来吗?并说明理由;
(3)在他们第二个发现的启发下,运用撘话?-特殊--一般數乃枷耄?慊鼓芊⑾质裁矗磕隳苡檬?в镅越?愕牟孪氡硎龀隼绰穑磕愕牟孪肽艹闪⒙穑咳裟艹闪ⅲ?胨得骼碛桑?/P>
查看答案和解析>>
科目:初中数学 来源:数学教研室 题型:044
(1)请你协助探求出当实数a变化时,抛物线y=ax2+2x+3的顶点所在直线的解析式;
(2)问题(1)中的直线上有一个点不是该抛物线的顶点,你能找出它来吗?并说明理由;
(3)在他们第二个发现的启发下,运用“一般——特殊——一般”的思想,你还能发现什么?你能用数学语言将你的猜想表述出来吗?你的猜想能成立吗?若能成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源:同步轻松练习 九年级数学下 题型:059
某学校研究性学习小组在研究二次函数及其图象的问题时,发现了两个重要结论:
①抛物线y=ax2+2x+3(a≠0),当实数a变化时,它的顶点都在某条直线上;
②抛物线y=ax2+2x+3的顶点横坐标减少![]() ,纵坐标增加
,纵坐标增加![]() 得到点A;顶点横坐标增加
得到点A;顶点横坐标增加![]() ,纵坐标增加
,纵坐标增加![]() 得到点B,则A,B两点仍然在抛物线y=ax2+2x+3上.
得到点B,则A,B两点仍然在抛物线y=ax2+2x+3上.
(1)探索当实数a变化时,抛物线y=ax2+2x+3的顶点所在直线的解析式;
(2)问题(1)中的直线上有一个点不是抛物线的顶点,请你找出来,并说明理由;
(3)请你参考第二个发现写出关于抛物线y=ax2+bx+c顶点的结论,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com