
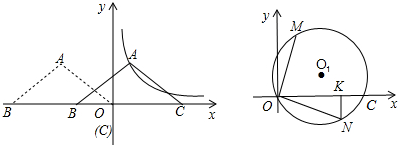
分析 (1)过点A作AH⊥OB于H,如图1,根据等腰三角形的性质得BH=OH=3,B(-6,0),由于点P平移纵坐标不变,则可确定平移后A点坐标为(1,2),然后根据平移的性质确定平移后B点坐标和C的坐标;
(2)作AM⊥y轴于M,如图1,根据三角形内心性质得∠BPM=∠APM,则可证明Rt△OPB∽△MPA,利用相似三角形的性质得$\frac{1}{2}$=$\frac{PO-2}{PO}$,解得OP=4,于是得到P点坐标为(0,4);
(3)过M点作MQ⊥y轴于Q,ME⊥x轴于E,连结MN、CM,如图2,先证明Rt△OMQ∽Rt△ONK得到$\frac{QM}{NK}$=$\frac{OM}{ON}$,再证明Rt△OMN∽Rt△EMC得到$\frac{OM}{ME}$=$\frac{ON}{CE}$,即$\frac{OM}{ON}$=$\frac{ME}{CE}$,所以$\frac{QM}{NK}$=$\frac{ME}{CE}$,利用比例性质易得NK=$\frac{3}{t}$,所以NK的长度随t的变化而变化.
解答 解:(1)过点A作AH⊥OB于H,如图1,
∵AB=AC,
∴BH=OH=3,
∴B(-6,0)
当y=2时,$\frac{2}{x}$=2,解得x=1,即平移后A点坐标为(1,2),
∴等腰△ABC沿x轴向右平移了4个单位,
∴平移后B点坐标为(-2,0)、C的坐标为(4,0);
(2)存在.
作AM⊥y轴于M,如图1,
∵△ABP的内心在y轴上
∴OP平分∠BPA,即∠BPM=∠APM,
∴Rt△OPB∽△MPA,
∴$\frac{AM}{OB}$=$\frac{PM}{PO}$,即$\frac{1}{2}$=$\frac{PO-2}{PO}$,解得OP=4,
∴P点坐标为(0,4);
(3)KN的长度的值变化.
过M点作MQ⊥y轴于Q,ME⊥x轴于E,连结MN、CM,如图2,
∵OM⊥ON,
∴∠MON=90°,即∠MOK+∠NOK=90°,
而∠MOK+∠MOQ=90°,
∴∠MOQ=∠NOK,
∴Rt△OMQ∽Rt△ONK,
∴$\frac{QM}{NK}$=$\frac{OM}{ON}$,
∵∠MCE=∠MNO,
∴Rt△OMN∽Rt△EMC,
∴$\frac{OM}{ME}$=$\frac{ON}{CE}$,即$\frac{OM}{ON}$=$\frac{ME}{CE}$,
∴$\frac{QM}{NK}$=$\frac{ME}{CE}$,即$\frac{1}{NK}$=$\frac{t}{4-1}$,
∴NK=$\frac{3}{t}$,
当t变化时,NK的长度也发生变化.
点评 本题考查了反比例函数综合题:熟练掌握反比例函数图象上点的坐标特征和等腰三角形的性质;理解坐标与图形性质;会运用相似三角形的求线段的长和判断线段之间的关系.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,AC⊥CB于C,CD⊥AB于D,下列关系中一定成立的是(3)(填序号)
如图,AC⊥CB于C,CD⊥AB于D,下列关系中一定成立的是(3)(填序号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 若点A、B分别表示2个居民小区,直线a表示公交通道,欲在其旁边建1个公交车站,且使从该站到2个小区的总路程最短,应如何确定车站的位置?请在图中画出来.
若点A、B分别表示2个居民小区,直线a表示公交通道,欲在其旁边建1个公交车站,且使从该站到2个小区的总路程最短,应如何确定车站的位置?请在图中画出来.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com