练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．下列说法不正确的是（　　）
    A．某种彩票中奖的概率是$\frac{1}{1000}$，买1000张彩票一定会中奖
    B．了解一种电器的使用寿命适合用抽样调查
    C．若A组数据的方差是0.31，B组数据的方差是0.25，则B组数据比A组数据稳定
    D．在一个装有白球和绿球的袋中摸球，摸出黑球是不可能事件

    分析 分别利用概率的意义以及抽样调查的意义以及方差的性质和随机事件的定义分别分析得出答案．

    解答 解：A、某种彩票中奖的概率是$\frac{1}{1000}$，买1000张彩票一定会中奖，错误，符合题意；
    B、了解一种电器的使用寿命适合用抽样调查，正确，不合题意；
    C、若A组数据的方差是0.31，B组数据的方差是0.25，则B组数据比A组数据稳定，正确，不合题意；
    D、在一个装有白球和绿球的袋中摸球，摸出黑球是不可能事件，正确，不合题意；
    故选：A．

    点评 此题主要考查了概率的意义以及抽样调查的意义以及方差的性质和随机事件的定义，正确把握相关性质是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    6．如图，在Rt△ABC中，已知∠BAC=90°，点D、E、F分别是三边的中点，若AF=3cm，则DE=3cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．已知2+$\frac{2}{3}$=22×$\frac{2}{3}$，3+$\frac{3}{8}$=32×$\frac{3}{8}$，4+$\frac{4}{15}$=42×$\frac{4}{15}$，…，且10+$\frac{a}{b}$=102×$\frac{a}{b}$（a，b均为正整数）．
    （1）探究a，b的值；
    （2）求分式$\frac{{a}^{2}+4ab+4{b}^{2}}{{a}^{2}+2ab}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．已知：在Rt△ABC中，∠C=90°，AC=6，BC=8，点E是边AC上一动点，过点E作EF∥BC，交AB边于点F，点D为BC上任一点，连接DE、DF，设EC长为x，则△DEF面积y关于x的函数图象大致为（　　）
    A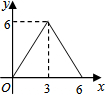．B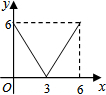．C．D．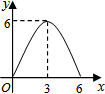

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．如图，A、D是⊙O上的两点，BC是直径，若∠D=35°，则∠OCA的度数是（　　）
    A．35°B．55°C．65°D．70°

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．下列说法正确的是（　　）
    A．掷一枚质地均匀的骰子，“向上一面的点数是6”是必然事件
    B．了解一批电视机的使用寿命，适合用普查的方式
    C．“明天降雨的概率为$\frac{1}{2}$”，表示明天有半天都在降雨
    D．在统计中，样本的方差可以近似地反映总体的波动大小

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．已知$\frac{n}{m}$=2，则$\frac{n}{n-m}$-$\frac{m}{n+m}$=1$\frac{2}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

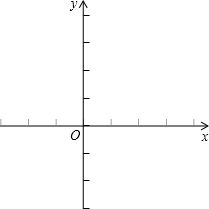    5．抛物线y=ax2-2ax-3a与x轴交于A、B两点（其中A在左侧，B在右侧，且经过点C（2，3）．
    （1）求抛物线解析式；
    （2）点D为线段AC上一动点（与A、C不重合），过D作直线EF∥y轴交抛物线于E．交x轴于F，请求出当DE最大时的E点坐标和DF长；
    （3）是否存在点E，使△DCE为等腰直角三角形？若存在，请求出点D的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

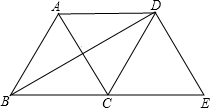    6．如图，将等边△ABC绕点C顺时针旋转120°得到△EDC，连接AD，BD．则下列结论：
    ①AC=AD；②BD⊥AC；③四边形ACED是菱形．
    其中正确的个数是（　　）
    A．0B．1C．2D．3

    查看答案和解析>>

    同步练习册答案