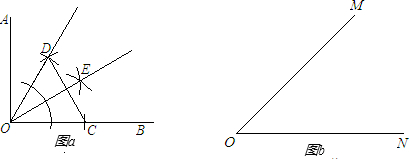练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    已知点A(
    1
    3
    ，
    1
    a
    )，B(
    1
    4
    ，
    1
    b
    )，C(
    1
    5
    ，
    1
    c
    )    满足
    a
    b+c
    =
    1
    3
    ，
    b
    a+c
    =
    1
    2
    ，则A、B、C三点的位置适合（　　）
    A、组成锐角三角形
    B、组成直角三角形
    C、组成钝角三角形
    D、在同一直线上
    分析：根据比例的性质：两个内项之积等于两个外项之积，b、c都用a表示出来，再用待定系数法求得直线AB的解析式，再看点C是否在直线AB上即可．
    解答：解：∵
    a
    b+c
    =
    1
    3
    ，
    ∴3a=b+c    ①
    又∵
    b
    a+c
    =
    1
    2
    ，
    ∴2b=a+c②，
    由①②得b=
    4
    3
    a，c=
    5
    3
    a，
    ∴A（
    1
    3
    ，
    1
    a
    ），B（
    1
    4
    ，
    3
    4a
    ），C（
    1
    5
    ，
    3
    5a
    ），
    设直线AB的解析式为y=kx+b，将点A、B的坐标代入，得k=
    3
    a
    ，b=0，
    ∴直线AB的解析式为y=
    3
    a
    x，
    将点C的坐标代入解析式，左边=右边，
    ∴A、B、C三点在一条直线上．
    故选D．
    点评：本题考查了用待定系数法求一次函数的解析式，是基础知识要熟练掌握，但此题难度较大．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    （1）“三等分角”是数学史上一个著名问题，但数学家已经证明，仅用尺规不可能“三等分任意角”．但对于特定度数的已知角，如90°角、45°角等，是可以用尺规进行三等分的．如图a，∠AOB=90°，我们在边OB上取一点C，用尺规以OC为一边向∠AOB内部作等边△OCD，作射线OD，再用尺规作出∠DOB的角平分线OE，则射线OD、OE将∠AOB三等分．仔细体会一下其中的道理，然后用尺规把图b中的∠MON三等分（已知∠MON=45°）．（不需写作法，但需保留作图痕迹，允许适当添加文字的说明）
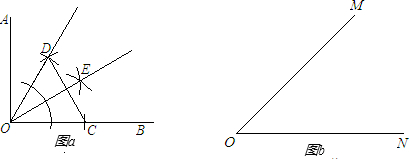
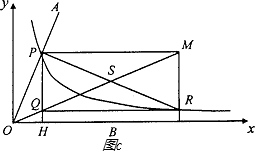
    精英家教网
    （2）数学家帕普斯借助函数给出了一种“三等分锐角”的方法（如图c）：将给定的锐角∠AOB置于直角坐标系中，边OB在x轴上、边OA与函数y=
    1
    x
    的图象交于点P，以P为圆心、2OP长为半径作弧交图象于点R．分别过点P和R作x轴和y轴的平行线，两直线相交于点M，连接OM得到∠MOB，则∠MOB=
    1
    3
    ∠AOB．要明白帕普斯的方法，请研究以下问题：
    ①设P（a，
    1
    a
    ）、R（b，
    1
    b
    ），求直线OM对应的函数关系式（用含a、b的代数式表示）．
    ②分别过点P和R作y轴和x轴的平行线，两直线相交于点Q．请说明Q点在直线OM上，并据此证明∠MOB=
    1
    3
    ∠AOB．
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

    已知点A(
    1
    3
    ，
    1
    a
    )，B(
    1
    4
    ，
    1
    b
    )，C(
    1
    5
    ，
    1
    c
    )    满足
    a
    b+c
    =
    1
    3
    ，
    b
    a+c
    =
    1
    2
    ，则A、B、C三点的位置适合（　　）
    A．组成锐角三角形B．组成直角三角形
    C．组成钝角三角形D．在同一直线上

    查看答案和解析>>

    同步练习册答案