



 天天向上一本好卷系列答案
天天向上一本好卷系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
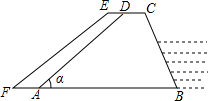 (2012•张家口一模)如图,梯形ABCD是一个拦河坝的截面图,坝高为6米.背水坡AD的坡度i为1:1.2,为了提高河坝的抗洪能力,防汛指挥部决定加固河坝,若坝顶CD加宽0.8米,新的背水坡EF的坡度为1:1.4.河坝总长度为4800米.
(2012•张家口一模)如图,梯形ABCD是一个拦河坝的截面图,坝高为6米.背水坡AD的坡度i为1:1.2,为了提高河坝的抗洪能力,防汛指挥部决定加固河坝,若坝顶CD加宽0.8米,新的背水坡EF的坡度为1:1.4.河坝总长度为4800米.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,阴影部分是一个新设计的徽章图案.图中正方形ABCD中,AD=2a,以点D为圆心,AD为半径作圆,与AD的延长线相交于点E,连结BE.则这个徽章图案(阴影部分)的面积等于
如图,阴影部分是一个新设计的徽章图案.图中正方形ABCD中,AD=2a,以点D为圆心,AD为半径作圆,与AD的延长线相交于点E,连结BE.则这个徽章图案(阴影部分)的面积等于查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com